5月14日,全都道府県に出されていた新型コロナウイルス対策緊急事態宣言が,39県で解除された。この中には13の特定警戒都道府県のうち,茨城県,石川県,愛知県,岐阜県,福岡県を含んでいる。ということで,北海道,東京都,神奈川県,埼玉県,千葉県,大阪府,兵庫県,京都府はおあずけだ。
しかし,大阪府は独自のモデルによる出口戦略の7日間連続条件が満たされたとして,休業要請の段階的な解除をはじめた。これに関する吉村の説明力は,あべちゃんのレベルをはるかに越えているので,支持者が増えるわけだ。これが維新ののしあがる契機となるのだとしたら,歴史はなんとひどいことをしてくれたものだということになるのかもしれない。
芥川龍之介が「蜘蛛の糸」を発表して百年。高二の秋の文化祭,クラスの仮装行列のテーマが 蜘蛛の糸だった。お釈迦様の極楽タワーの竹を近所から切り出し,地獄の焔と煙の絵を描いた。犍陀多に続いて蜘蛛の糸(登山部の赤いザイル)に群がる地獄の亡者だったころ。
2020年5月14日木曜日
2020年5月13日水曜日
パトカー
駐車場の入口付近に放置自転車が2週間ほど滞在されていて,車の出し入れに不都合があるということで,駐車場のオーナーに1週間ほど前に連絡差し上げるも,状況が変化しなかったので,天理警察署に防犯登録番号と車体番号と事情を連絡したところ,早速パトカーで3名のマスク警察官が見に来て下さったのであるが,調べていただいた結果,盗難届は出ておらず所有者の電話番号も使われていないということで,あとは,駐車場の管理者に連絡して処分しもらって下さいという,ウェブで検索したようなご回答をいただいたのであり,こちらとしても,この忙しい時期にわざわざ出向いていただいたことに,手厚くお礼を申し上げながら,この案件が終了してしまった。チーン。
2020年5月12日火曜日
えっ,この非常時にさえICTを使わないのなぜ?
文部科学省の令和2年度ICT活用アドバイザー事業「学校の情報環境整備に関する説明会(当日資料)」が5月11日(月)に開催され,youtubeでも配信されていた。また,まさきとみずもとかづきさんによるnoteで一部(重要な部分)が文字おこしされている。
文部科学省初等中等教育局情報教育・外国語教育課長の髙谷浩樹さんの説明はなかなか気合いが入っていた。配布資料にはなかったが,以下の部分がキモでした。
これからはICTを使わないことに説明責任が伴う(地方自治体に向けて),説明責任が伴うのは本件の文部科学省の私であり地方教育行政をになうあなた達である。我々は一蓮托生なのである。今までが間違っていたのだ。やろうとしないのは子どもに対する罪である。
豊福晋平さんは辛口のコメントをしていたが,みんながんばってほしい。
文部科学省初等中等教育局情報教育・外国語教育課長の髙谷浩樹さんの説明はなかなか気合いが入っていた。配布資料にはなかったが,以下の部分がキモでした。
図 高谷課長の声が聞こえてきた
豊福晋平さんは辛口のコメントをしていたが,みんながんばってほしい。
2020年5月11日月曜日
ヨビノリ(2)
ヨビノリ(1)からの続き
去年この記事を書いたのは教育系YouTuberがちょっと話題になっていたころだった。今日は,ヨビノリたくみさんが,2020年の2月14日に文部科学省で開かれた政策立案教養研修で講演しているYou Tube番組に行き当たった。なかなか参考になった。
この時点でのチャンネル登録者が30万人(その3ヶ月後の現在は42.5万人に達しているのだ。新型コロナウイルス感染症がもたらすオンライン教育への地殻変動の大きさがわかる),動画本数が400本,平均再生回数13万回/日,総再生回数3300万回(今日の時点では5000万回近くになっている)。
大学の理系学部の授業のシラバスに掲載され,参考資料としての活用が促されているようだ。また,視聴者層は,中高生20%,大学生・大学院生40%,社会人40%となっている。先端研究者(大学教員)へのインタビューや,ノーベル賞の説明など,幅広くこのニッチ市場を開拓している。また,ヨビノリはヨビノリたくみ+ヨビノリやすで構成されていたことをあらためて認識した。
自分でオンライン授業のためのノート+音声の紙芝居コンテンツを毎日3科目分つくってみると,ヨビノリコンテンツがさすがによくできていることを改めて感じることになった今日この頃。
去年この記事を書いたのは教育系YouTuberがちょっと話題になっていたころだった。今日は,ヨビノリたくみさんが,2020年の2月14日に文部科学省で開かれた政策立案教養研修で講演しているYou Tube番組に行き当たった。なかなか参考になった。
この時点でのチャンネル登録者が30万人(その3ヶ月後の現在は42.5万人に達しているのだ。新型コロナウイルス感染症がもたらすオンライン教育への地殻変動の大きさがわかる),動画本数が400本,平均再生回数13万回/日,総再生回数3300万回(今日の時点では5000万回近くになっている)。
大学の理系学部の授業のシラバスに掲載され,参考資料としての活用が促されているようだ。また,視聴者層は,中高生20%,大学生・大学院生40%,社会人40%となっている。先端研究者(大学教員)へのインタビューや,ノーベル賞の説明など,幅広くこのニッチ市場を開拓している。また,ヨビノリはヨビノリたくみ+ヨビノリやすで構成されていたことをあらためて認識した。
自分でオンライン授業のためのノート+音声の紙芝居コンテンツを毎日3科目分つくってみると,ヨビノリコンテンツがさすがによくできていることを改めて感じることになった今日この頃。
2020年5月10日日曜日
検察庁法改正案に反対する
twitterでのハッシュタグ署名「#検察庁法改正案に抗議します」が380万件を越えたようだ(NHK 2020.5.10 17:00ごろの記事にて※)。
森友−加計−桜などの一連の流れの総決算で,自民−公明−維新が国会の強行突破を図っている。ひどい話である。制度としても非常に大きな問題をかかえてしまう。
検察庁法は検察庁の組織と検察官の任免の手続きを定めている。今回の改正案は,国家公務員法等の一部を改正する法律案の中にあって,その問題点のキモは,「役職定年を導入し,検事正については法務大臣の判断,次長検事および検事長については内閣の判断で,個別に役職定年を延長することができるようにしたところ(なお,現在の検察庁法には役職定年の制度はない)」のようだ。
※その後400万件を越えたあたりで, https://twittrend.jp からは消されてしまったようだ。あいかわらず,twitter.jpの恣意的・政治的な運営は本当にひどいことになっている。その痕跡が図の地域別の一部に残っているという指摘があった。
[1]検事長の勤務延長に関する閣議決定の撤回を求め、国家公務員法等の一部を改正する法律案に反対する会長声明|あらためて検察庁法の一部改正に反対する会長声明(日本弁護士連合会)
[2]我が国の検察制度の特色(検察庁)
[3]いったい検察庁法改正案の何に抗議しているのか(徐東輝)
[4]安倍首相による 検察,警察の私物化−新型コロナ危機の陰で進む民主主義・法の支配の崩壊(小西洋之)
[5]「#検察庁法改正案に抗議します」をめぐって知っておいてほしいこと(山尾志桜里)
[6]twittrend(各地域のついっトレンド)
[7]twitter trending hashtag (こちらは改竄されておらず,約550万件に到達)
森友−加計−桜などの一連の流れの総決算で,自民−公明−維新が国会の強行突破を図っている。ひどい話である。制度としても非常に大きな問題をかかえてしまう。
検察庁法は検察庁の組織と検察官の任免の手続きを定めている。今回の改正案は,国家公務員法等の一部を改正する法律案の中にあって,その問題点のキモは,「役職定年を導入し,検事正については法務大臣の判断,次長検事および検事長については内閣の判断で,個別に役職定年を延長することができるようにしたところ(なお,現在の検察庁法には役職定年の制度はない)」のようだ。
第四条 検察庁法(昭和二十二年法律第六十一号)の一部を次のように改正する。などのあたりだろうか。
・・・
法務大臣は、前項の規定にかかわらず、年齢が六十三年に達した検事正の職を占める検事について、当該検事の職務の遂行上の特別の事情を勘案して、当該検事を他の職に補することにより公務の運営に著しい支障が生ずると認められる事由として法務大臣が定める準則(以下この条において単に「準則」という。)で定める事由があると認めるときは、当該検事が年齢六十三年に達した日の翌日から起算して一年を超えない範囲内で期限を定め、引き続き当該検事に、当該検事が年齢六十三年に達した日において占めていた職を占めたまま勤務をさせることができる。
法務大臣は、前項の期限又はこの項の規定により延長した期限が到来する場合において、前項の事由が引き続きあると認めるときは、準則で定めるところにより、これらの期限の翌日から起算して一年を超えない範囲内(その範囲内に定年に達する日がある検事にあつては、延長した期限の翌日から当該定年に達する日までの範囲内)で期限を延長することができる。
・・・
内閣は、前項の規定にかかわらず、年齢が六十三年に達した次長検事又は検事長について、当該次長検事又は検事長の職務の遂行上の特別の事情を勘案して、当該次長検事又は検事長を検事に任命することにより公務の運営に著しい支障が生ずると認められる事由として内閣が定める事由があると認めるときは、当該次長検事又は検事長が年齢六十三年に達した日の翌日から起算して一年を超えない範囲内で期限を定め、引き続き当該次長検事又は検事長に、当該次長検事又は検事長が年齢六十三年に達した日において占めていた官及び職を占めたまま勤務をさせることができる。
内閣は、前項の期限又はこの項の規定により延長した期限が到来する場合において、前項の事由が引き続きあると認めるときは、内閣の定めるところにより、これらの期限の翌日から起算して一年を超えない範囲内(その範囲内に定年に達する日がある次長検事又は検事長にあつては、延長した期限の翌日から当該定年に達する日までの範囲内)で期限を延長することができる。
図 twitterndにみられるtwitter改竄の痕跡?(左ビフォアー,右アフター)
※その後400万件を越えたあたりで, https://twittrend.jp からは消されてしまったようだ。あいかわらず,twitter.jpの恣意的・政治的な運営は本当にひどいことになっている。その痕跡が図の地域別の一部に残っているという指摘があった。
[1]検事長の勤務延長に関する閣議決定の撤回を求め、国家公務員法等の一部を改正する法律案に反対する会長声明|あらためて検察庁法の一部改正に反対する会長声明(日本弁護士連合会)
[2]我が国の検察制度の特色(検察庁)
[3]いったい検察庁法改正案の何に抗議しているのか(徐東輝)
[4]安倍首相による 検察,警察の私物化−新型コロナ危機の陰で進む民主主義・法の支配の崩壊(小西洋之)
[5]「#検察庁法改正案に抗議します」をめぐって知っておいてほしいこと(山尾志桜里)
[6]twittrend(各地域のついっトレンド)
[7]twitter trending hashtag (こちらは改竄されておらず,約550万件に到達)
2020年5月9日土曜日
ハナノナ
このところCOVID-19の話ばかり書いてきたのでちょっと食傷気味である。
今日は別の話題です。「無料でカメラを向けた花の名前を即座にAIが教えてくれるアプリハナノナを使ってみた」という記事があったのでさっそくiPhoneにインストールしたところ,なかなかすごいのだった。ベランダのムラサキカタバミを早速言い当てた。
千葉工業大学のステアラボ(人工知能・ソフトウェア技術研究センター)で2017年に開発されたものらしい。ウエブサービスハナノナとして始まった。最近,認識できる花の種類のが770種類にまでアップデートされ,iPhoneアプリも登場した。この手のアプリはのどから手が出るほどほしかった。まあ,ないことはなかったのです。これまでに,京都大学発祥?のいきものコレクションアプリBIOMEを使ったこともあるのだけれど,機能を欲張りすぎた割には精度がいまいちで,アプリ画面のこやしになっていた。
その点,ハナノナは単純な機能がよいのである(草木にも拡張してほしい)。この調子でトリノナ(鳥類),ムシノナ(節足動物・両生類・爬虫類),クモノナ(雲です),ホシノナ(☆です),イシノナ(岩石鉱物),トモノナ(ホ乳類),ウオノナ(魚類・水生生物)など作っていただけるとうれしいなあ。これらができた後でモノノナ(万物)に統合されるのはOKです。これで小学校の理科はOKです。
今日は別の話題です。「無料でカメラを向けた花の名前を即座にAIが教えてくれるアプリハナノナを使ってみた」という記事があったのでさっそくiPhoneにインストールしたところ,なかなかすごいのだった。ベランダのムラサキカタバミを早速言い当てた。
千葉工業大学のステアラボ(人工知能・ソフトウェア技術研究センター)で2017年に開発されたものらしい。ウエブサービスハナノナとして始まった。最近,認識できる花の種類のが770種類にまでアップデートされ,iPhoneアプリも登場した。この手のアプリはのどから手が出るほどほしかった。まあ,ないことはなかったのです。これまでに,京都大学発祥?のいきものコレクションアプリBIOMEを使ったこともあるのだけれど,機能を欲張りすぎた割には精度がいまいちで,アプリ画面のこやしになっていた。
その点,ハナノナは単純な機能がよいのである(草木にも拡張してほしい)。この調子でトリノナ(鳥類),ムシノナ(節足動物・両生類・爬虫類),クモノナ(雲です),ホシノナ(☆です),イシノナ(岩石鉱物),トモノナ(ホ乳類),ウオノナ(魚類・水生生物)など作っていただけるとうれしいなあ。これらができた後でモノノナ(万物)に統合されるのはOKです。これで小学校の理科はOKです。
図 本日の朝の散歩におけるハナノナの成果の一部(2020.5.9撮影)
追伸:モノノナのイメージが出てきた。目に映るものの名前をできる限り知りたい(デイリーポータル,2020.05.22)
2020年5月8日金曜日
小田垣さんのSIQR
朝日新聞に,九州大学名誉教授の小田垣さんの計算として「PCR検査を倍にすれば、接触「5割減」でも収束可能?」という記事がでた。twitterでも注目を集めていた。
小田垣さんのホームページにその論考があった[1]。SIQRモデルということで,感染者を2段階に分けていた。我々のSIIDR2モデルと本質的に同じではないか。感受性保持者S(t)から直接我々の重症患者I2(t),すなわち小田垣さんの隔離感染者Q(t)に遷移する項があって,ここは違うのだが,議論が始まる前の段階でこの項を落としているので結局同じです。違うのはこちらには死亡数D(t)への遷移を含んでいることくらいである。
そこで両方のモデルで使用しているパラメタを比較してみた。左が小田垣さんのSIQR,右が我々のSIIDR2である。
\begin{equation}
\begin{aligned}
N\beta \quad (0.07) &= \beta \quad (0.4-0.6) \\
p \quad (0.096) &= \dfrac{1}{\alpha_2} \quad (0.04) \\
\gamma \quad (0.04) &= \dfrac{1}{\alpha_1} \quad (0.16) \\
\gamma \quad (0.04) &= \dfrac{1}{\gamma_1}\quad (0.064) \\
noparameter (0) &= \dfrac{1}{\gamma_2}\quad (0.00267) \\
\end{aligned}
\end{equation}
感染率の$\beta$が一桁違うことがわかる。その他はファクターが異なるくらいである。I(t)からR(t)への遷移時間とQ(t)からR(t)への遷移時間が同じとしていることもやや疑問に感じる。また,小田垣氏は論考の中で,基本再生産数(実効再生産数)は$N\beta/p$でなく$N\beta/(p+\gamma)$とすべきだと主張しているが,これはどうなのだろうか。
とりあえず,感染初期のS(t)=Nのときにあてはめて,接触5割減の議論に持ち込んでいる部分は興味深いが,実際にこのパラメータを使って日本の感染データの全体像を説明できるのだろうか。我々のコードを少し修正して彼らのモデルとパラメタを使った計算を再現してみた(初期値の細かな調整は我々のモデルを前提としているがとりあえずはそこはそのままにしておく)。
- - - - - - - - - - - - - - - - - - - - - - - - - - - - -
using DifferentialEquations
using ParameterizedFunctions
using Plots; gr()
sky = @ode_def SIQR_model begin
du0 = 1 # u0:time
du1 = -β*u1*u2/n # u1:Noimmunity(Susceptible)
du2 = β*u1*u2/n -u2/α2 -u2/α1 # u2:(Infected)
du3 = u2/α2 -u3/γ1 # u3:(Quarantined)
du4 = u3/γ2 # u4:Dead(not in use)
du5 = u2/α1 +u3/γ1 # u5:Recovered
du6 = u2/α2 # u6:Accumulated Quarantined
du7 = u3/γ1 # u7:Accululated Recovered
end n α1 α2 β γ1 γ2 λ τ
function epidm(β,ν,λ,τ,T)
n=10000.0 #total number of population
α1=1/0.04 #5.0/0.8 #latent to recovery (days/%)
α2=1/0.096 #5.0/0.2 #latent to onset (days/%)
β=0.07 #0.45 #infection rate (/day・person)
γ1=1/0.04 #15.0/0.96 #onset to recovery (days/%)
γ2=15.0/0.04 #onset to death (days/%) (not in use)
u0 = [0.0,n-11ν,4ν,2ν,0.0,5ν,ν,0.0] #initial values
p = (n,α1,α2,β,γ1,γ2,λ,τ) #parameters
tspan = (0.0,T) #time span in days
prob = ODEProblem(sky,u0,tspan,p)
sol = solve(prob)
return sol
end
#japan-data(start=3/1)
xj=[0,1,2,3,4,5,6,7,8,9,10,11,12,13,
14,15,16,17,18,19,20,21,22,23,24,25,26,27,
28,29,30,31,32,33,34,35,36,37,38,39,40,41,
42,43,44,45,46,47,48,49,50,51,52,53,54,55,
56,57,58,59,60,61,62]
yj=[0.0190,0.0202,0.0213,0.0225,0.0252,0.0277,0.0324,
0.0361,0.0387,0.0408,0.0451,0.0492,0.0536,0.0568,
0.0619,0.0646,0.0658,0.0658,0.0693,0.0754,0.0790,
0.0830,0.0864,0.0895,0.0947,0.103,0.110,0.119,
0.134,0.148,0.155,0.173,0.189,0.208,0.232,
0.260,0.290,0.310,0.338,0.378,0.424,0.477,
0.536,0.576,0.607,0.643,0.681,0.728,0.777,
0.822,0.853,0.882,0.912,0.946,0.983,1.018,
1.046,1.062,1.078,1.099,1.118,1.133,1.154]
zj=[0.040,0.048,0.048,0.048,0.048,0.048,0.048,
0.048,0.056,0.071,0.095,0.119,0.151,0.167,
0.175,0.190,0.222,0.222,0.230,0.262,0.278,
0.286,0.325,0.333,0.341,0.357,0.365,0.389,
0.413,0.429,0.444,0.452,0.452,0.516,0.548,
0.556,0.579,0.635,0.643,0.675,0.698,0.746,
0.778,0.810,0.865,0.944,1.079,1.175,1.222,
1.278,1.357,1.476,2.198,2.278,2.516,2.651,
2.762,2.786,2.984,3.087,3.294,3.429,3.603]/100
plot(xj,yj,st=:scatter,label="Confirmed-japan")
#plot!(xj,zj,st=:scatter,label="Deaths-japan")
β=0.07
ν=0.01
T=60
@time so=epidm(β,ν,λ,τ,T)
#plot!(so,vars=(0,2))
#plot!(so,vars=(0,3))
plot!(so,vars=(0,4))
#plot!(so,vars=(0,5))
#plot!(so,vars=(0,6))
plot!(so,vars=(0,7))
- - - - - - - - - - - - - - - - - - - - - - - - - - - - -
[1]新型コロナウイルスの蔓延に関する一考察(小田垣孝,2020.5.5)
[2]隔離と市中の感染者を分ける SIR モデル(佐野雅己,2020.4.29)
[3]3.11以後の科学リテラシー No. 89(牧野淳一郎,2020 科学5月号)
[4]感染症の数理シミュレーション(8)(2020.3.15)
小田垣さんのホームページにその論考があった[1]。SIQRモデルということで,感染者を2段階に分けていた。我々のSIIDR2モデルと本質的に同じではないか。感受性保持者S(t)から直接我々の重症患者I2(t),すなわち小田垣さんの隔離感染者Q(t)に遷移する項があって,ここは違うのだが,議論が始まる前の段階でこの項を落としているので結局同じです。違うのはこちらには死亡数D(t)への遷移を含んでいることくらいである。
そこで両方のモデルで使用しているパラメタを比較してみた。左が小田垣さんのSIQR,右が我々のSIIDR2である。
\begin{equation}
\begin{aligned}
N\beta \quad (0.07) &= \beta \quad (0.4-0.6) \\
p \quad (0.096) &= \dfrac{1}{\alpha_2} \quad (0.04) \\
\gamma \quad (0.04) &= \dfrac{1}{\alpha_1} \quad (0.16) \\
\gamma \quad (0.04) &= \dfrac{1}{\gamma_1}\quad (0.064) \\
noparameter (0) &= \dfrac{1}{\gamma_2}\quad (0.00267) \\
\end{aligned}
\end{equation}
感染率の$\beta$が一桁違うことがわかる。その他はファクターが異なるくらいである。I(t)からR(t)への遷移時間とQ(t)からR(t)への遷移時間が同じとしていることもやや疑問に感じる。また,小田垣氏は論考の中で,基本再生産数(実効再生産数)は$N\beta/p$でなく$N\beta/(p+\gamma)$とすべきだと主張しているが,これはどうなのだろうか。
とりあえず,感染初期のS(t)=Nのときにあてはめて,接触5割減の議論に持ち込んでいる部分は興味深いが,実際にこのパラメータを使って日本の感染データの全体像を説明できるのだろうか。我々のコードを少し修正して彼らのモデルとパラメタを使った計算を再現してみた(初期値の細かな調整は我々のモデルを前提としているがとりあえずはそこはそのままにしておく)。
- - - - - - - - - - - - - - - - - - - - - - - - - - - - -
using DifferentialEquations
using ParameterizedFunctions
using Plots; gr()
sky = @ode_def SIQR_model begin
du0 = 1 # u0:time
du1 = -β*u1*u2/n # u1:Noimmunity(Susceptible)
du2 = β*u1*u2/n -u2/α2 -u2/α1 # u2:(Infected)
du3 = u2/α2 -u3/γ1 # u3:(Quarantined)
du4 = u3/γ2 # u4:Dead(not in use)
du5 = u2/α1 +u3/γ1 # u5:Recovered
du6 = u2/α2 # u6:Accumulated Quarantined
du7 = u3/γ1 # u7:Accululated Recovered
end n α1 α2 β γ1 γ2 λ τ
function epidm(β,ν,λ,τ,T)
n=10000.0 #total number of population
α1=1/0.04 #5.0/0.8 #latent to recovery (days/%)
α2=1/0.096 #5.0/0.2 #latent to onset (days/%)
β=0.07 #0.45 #infection rate (/day・person)
γ1=1/0.04 #15.0/0.96 #onset to recovery (days/%)
γ2=15.0/0.04 #onset to death (days/%) (not in use)
u0 = [0.0,n-11ν,4ν,2ν,0.0,5ν,ν,0.0] #initial values
p = (n,α1,α2,β,γ1,γ2,λ,τ) #parameters
tspan = (0.0,T) #time span in days
prob = ODEProblem(sky,u0,tspan,p)
sol = solve(prob)
return sol
end
#japan-data(start=3/1)
xj=[0,1,2,3,4,5,6,7,8,9,10,11,12,13,
14,15,16,17,18,19,20,21,22,23,24,25,26,27,
28,29,30,31,32,33,34,35,36,37,38,39,40,41,
42,43,44,45,46,47,48,49,50,51,52,53,54,55,
56,57,58,59,60,61,62]
yj=[0.0190,0.0202,0.0213,0.0225,0.0252,0.0277,0.0324,
0.0361,0.0387,0.0408,0.0451,0.0492,0.0536,0.0568,
0.0619,0.0646,0.0658,0.0658,0.0693,0.0754,0.0790,
0.0830,0.0864,0.0895,0.0947,0.103,0.110,0.119,
0.134,0.148,0.155,0.173,0.189,0.208,0.232,
0.260,0.290,0.310,0.338,0.378,0.424,0.477,
0.536,0.576,0.607,0.643,0.681,0.728,0.777,
0.822,0.853,0.882,0.912,0.946,0.983,1.018,
1.046,1.062,1.078,1.099,1.118,1.133,1.154]
zj=[0.040,0.048,0.048,0.048,0.048,0.048,0.048,
0.048,0.056,0.071,0.095,0.119,0.151,0.167,
0.175,0.190,0.222,0.222,0.230,0.262,0.278,
0.286,0.325,0.333,0.341,0.357,0.365,0.389,
0.413,0.429,0.444,0.452,0.452,0.516,0.548,
0.556,0.579,0.635,0.643,0.675,0.698,0.746,
0.778,0.810,0.865,0.944,1.079,1.175,1.222,
1.278,1.357,1.476,2.198,2.278,2.516,2.651,
2.762,2.786,2.984,3.087,3.294,3.429,3.603]/100
plot(xj,yj,st=:scatter,label="Confirmed-japan")
#plot!(xj,zj,st=:scatter,label="Deaths-japan")
β=0.07
ν=0.01
T=60
@time so=epidm(β,ν,λ,τ,T)
#plot!(so,vars=(0,2))
#plot!(so,vars=(0,3))
plot!(so,vars=(0,4))
#plot!(so,vars=(0,5))
#plot!(so,vars=(0,6))
plot!(so,vars=(0,7))
- - - - - - - - - - - - - - - - - - - - - - - - - - - - -
結果は以下の通りである。確かに初期の段階ではデータを説明しているが,その後の振る舞いは説明できない。このモデル(のパラメタ)はあまりよろしくないのかもしれない。
[1]新型コロナウイルスの蔓延に関する一考察(小田垣孝,2020.5.5)
[2]隔離と市中の感染者を分ける SIR モデル(佐野雅己,2020.4.29)
[3]3.11以後の科学リテラシー No. 89(牧野淳一郎,2020 科学5月号)
[4]感染症の数理シミュレーション(8)(2020.3.15)
2020年5月7日木曜日
中野さんのK値
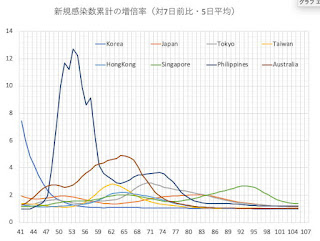
阪大の杉山清寛さんのFacebookから,RCNPの中野貴志さん(ペンタクオークでおなじみ)がCOVID-19の収束状況を判定するK値というのを考案しているという情報がみつかった。あれ,こちらで計算していたものと本質的に同じ量ではないか。彼のK値は次式で与えられる[2]。総感染者数は我々の(というか普通報道されている)新規感染数累計(Confirmed)のことだ。3月の末に,新規感染数累計の増倍率という記事[1]を書いていた(忘れていた)。
K = 1 - (1週間前の総感染者数) / (当日の総感染者数)
こちらで計算を続けていたのは,r = (当日の総感染者数)/ (1週間前の総感染者数) = 1/(1-K) である。最近1に収束してきて(下に有界な単調減少数列)おもしろい情報がとれないので更新を停止したところであった。なるほど,こうすれば,初期段階の感度は悪いが,収束段階の感度はよくなる。また,中野さんの最近の論考[3]ではさらに考察が進化していた。まあ,物理屋さんがやるとだいたいこういう発想になるのだろう。
その3月下旬から4月にかけて日本だけが他の国と違う振る舞いを見せていてどきどきしたが,やがて収まった。逆にシンガポールの異常を発見したのもこれを観察していたときだった。
[1]新規感染数累計の増倍率(2020.3.31)
[2]COVID-19 感染状況の推移について(中野貴志,2020.4.19)
[3]K 値で読み解く COVID-19 の感染状況と今後の推移(中野貴志・池田陽一,2020.5.6)
[4]新型コロナウイルス感染症(COVID-19)について(吉森保,2020.5.10)
K = 1 - (1週間前の総感染者数) / (当日の総感染者数)
こちらで計算を続けていたのは,r = (当日の総感染者数)/ (1週間前の総感染者数) = 1/(1-K) である。最近1に収束してきて(下に有界な単調減少数列)おもしろい情報がとれないので更新を停止したところであった。なるほど,こうすれば,初期段階の感度は悪いが,収束段階の感度はよくなる。また,中野さんの最近の論考[3]ではさらに考察が進化していた。まあ,物理屋さんがやるとだいたいこういう発想になるのだろう。
図1 アジアの新規感染数累計増倍率の推移(2020.3.1-5.4)
図2 ヨーロッパの新規感染数累計増倍率の推移(2020.3.9-5.4)
その3月下旬から4月にかけて日本だけが他の国と違う振る舞いを見せていてどきどきしたが,やがて収まった。逆にシンガポールの異常を発見したのもこれを観察していたときだった。
[1]新規感染数累計の増倍率(2020.3.31)
[2]COVID-19 感染状況の推移について(中野貴志,2020.4.19)
[3]K 値で読み解く COVID-19 の感染状況と今後の推移(中野貴志・池田陽一,2020.5.6)
[4]新型コロナウイルス感染症(COVID-19)について(吉森保,2020.5.10)
2020年5月6日水曜日
米国の集団免疫率(3)
米国の集団免疫率(2)からの続き
タイトルはもう変更したほうがいいかもしれない。というのも,抗体検査の結果,ニューヨーク州では12.3%が抗体を持っている(感染済)という結果がでているからだ。こちらの結果とはほぼ1桁違うので,我々のモデルの前提や仮定のどれかががまったく間違っているのではないか。しかし,モデルを検討する余力がないので(遠隔授業の準備で手いっぱい),そこは放置したまま,米国の新しいデータに基づいたパラメタ推定を行う。というのも,これまでの6万人から6.5万人という発表に代わり,再び死亡者が10万人を越えるという予想が出ているからだ。前回と同様に,HEMLのCOVID-19 projections のページを見れば,確かに米国全体の死亡数は8月には13.4万人になりそうだとある。
前回同様のSIIDR2モデルで計算する。使用するWHOのデータ(人口1万人当り)はこれ。
- - - - - - - - - - - - - - - - - - - - - - - - - - - - -
ya=[0.014,0.021,0.030,0.038,0.051,0.051,0.051,
0.106,0.107,0.215,0.317,0.462,0.462,0.958,
1.280,1.576,1.929,2.074,2.587,3.136,3.722,
4.268,4.953,5.684,6.483,7.335,8.310,9.327,
10.13,11.03,11.99,12.93,14.00,14.96,15.92,
16.81,17.55,18.33,19.20,20.19,21.10,21.96,
22.80,23.58,24.31,25.19,26.12,27.29,28.28,
29.16,29.85,30.47,31.42,32.39,33.20,34.16]
za=[0.0006,0.0008,0.0009,0.0011,0.0012,0.0012,0.0012,
0.0018,0.0018,0.0030,0.0046,0.0061,0.0061,0.0122,
0.0143,0.0204,0.0268,0.0301,0.0377,0.0506,0.0641,
0.0728,0.0865,0.117,0.146,0.178,0.213,0.254,
0.290,0.329,0.387,0.445,0.504,0.562,0.620,
0.667,0.712,0.785,0.856,0.922,0.984,1.038,
1.089,1.141,1.216,1.284,1.337,1.402,1.456,
1.492,1.532,1.591,1.679,1.742,1.792,1.842]
- - - - - - - - - - - - - - - - - - - - - - - - - - - - -
P. S. 日本でも,神戸の病院の外来患者の約3%に新型コロナウイルス感染症の抗体が検出されたとある。なかなか大きな数字だ。これが1%だとしても,大都市部の数十万人が感染済みということ。
タイトルはもう変更したほうがいいかもしれない。というのも,抗体検査の結果,ニューヨーク州では12.3%が抗体を持っている(感染済)という結果がでているからだ。こちらの結果とはほぼ1桁違うので,我々のモデルの前提や仮定のどれかががまったく間違っているのではないか。しかし,モデルを検討する余力がないので(遠隔授業の準備で手いっぱい),そこは放置したまま,米国の新しいデータに基づいたパラメタ推定を行う。というのも,これまでの6万人から6.5万人という発表に代わり,再び死亡者が10万人を越えるという予想が出ているからだ。前回と同様に,HEMLのCOVID-19 projections のページを見れば,確かに米国全体の死亡数は8月には13.4万人になりそうだとある。
前回同様のSIIDR2モデルで計算する。使用するWHOのデータ(人口1万人当り)はこれ。
- - - - - - - - - - - - - - - - - - - - - - - - - - - - -
ya=[0.014,0.021,0.030,0.038,0.051,0.051,0.051,
0.106,0.107,0.215,0.317,0.462,0.462,0.958,
1.280,1.576,1.929,2.074,2.587,3.136,3.722,
4.268,4.953,5.684,6.483,7.335,8.310,9.327,
10.13,11.03,11.99,12.93,14.00,14.96,15.92,
16.81,17.55,18.33,19.20,20.19,21.10,21.96,
22.80,23.58,24.31,25.19,26.12,27.29,28.28,
29.16,29.85,30.47,31.42,32.39,33.20,34.16]
za=[0.0006,0.0008,0.0009,0.0011,0.0012,0.0012,0.0012,
0.0018,0.0018,0.0030,0.0046,0.0061,0.0061,0.0122,
0.0143,0.0204,0.0268,0.0301,0.0377,0.0506,0.0641,
0.0728,0.0865,0.117,0.146,0.178,0.213,0.254,
0.290,0.329,0.387,0.445,0.504,0.562,0.620,
0.667,0.712,0.785,0.856,0.922,0.984,1.038,
1.089,1.141,1.216,1.284,1.337,1.402,1.456,
1.492,1.532,1.591,1.679,1.742,1.792,1.842]
- - - - - - - - - - - - - - - - - - - - - - - - - - - - -
パラメタはこれ,前回と少し変えている。
#β=0.61,ν=0.12,λ=49,τ=16,α2=5.0/0.20,γ2†=15.0/0.10
結果はこれ,確かに15〜16万人くらいになりそうだ。
図 米国の感染カーブ(u3=重症感染数,u4=死亡数,u6=新規感染数累計,1万人当)
2020年5月5日火曜日
CFR(致命率)(1)
一つの集団におけるある感染症の致命率(Case Fatality Rate)とは,その集団における感染者数に対する,その感染症が原因となる死亡者数の比率である。COVID-19における各国の致命率の時間推移が次のサイトMotality Risk of COVID-19 (Our World in Data)にある。そこでいくつかの代表的な国々を選んで図示してみた。
図 各国のCFRの推移(3/20-5/2)
アジアが欧米に比べて明らかに低いのは何故かという問題提起があったが,これをみれば,米国と中国は同じオーダーである。ここに載せていない,台湾,香港,シンガポールが非常に小さいのは確かである。
2020年5月4日月曜日
新型コロナ感染症の時系列
自分で計算できる実効再生産数からの続き
高橋健太郎さんが12日シフトで説明できるということだったので,これまでの経緯を時系列でまとめ,前回の実効再生産数の計算値の日付を12日だけ引き算した日時にあてはめてならべてみたものを,日付[数値]として埋め込んだ表を作った。
- - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
1/30 新型コロナウイルス感染症対策本部の設置
2/04 ダイヤモンドプリンセス横浜で再検疫
2/16 [1.0]
2/19 ダイヤモンドプリンセス下船開始
2/21 [2.1]
2/26 全国的イベント自粛(Perfume EXILE)
2/29 [1.1]
3/01 ダイヤモンドプリンセス全員下船
2/28 北海道知事の緊急事態宣言
3/02 要請に基づく全国学校休業(-春休み)
3/05 [1.0]
3/08 大相撲無観客場所初日
3/13 [2.1]
3/14 新型インフルエンザ等対策特別措置法改正
3/17 特措法にもとづく新型コロナウイルス感染症対策本部へ
3/20 [1.7]
3/24 東京五輪を2021年に延期
3/25 東京都重要局面発言/春休み
3/28 [1.5]
3/29 志村けん
3/31 [1.0]
4/05 [1.0]
4/07 7都府県に特措法による緊急事態宣言(-5/6)
4/16 [0.5]
4/16 全国に特措法による緊急事態宣言(-5/6)
5/04 全国の緊急事態宣言延長(-5/31)
- - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
高橋健太郎さんが12日シフトで説明できるということだったので,これまでの経緯を時系列でまとめ,前回の実効再生産数の計算値の日付を12日だけ引き算した日時にあてはめてならべてみたものを,日付[数値]として埋め込んだ表を作った。
- - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
1/30 新型コロナウイルス感染症対策本部の設置
2/04 ダイヤモンドプリンセス横浜で再検疫
2/16 [1.0]
2/19 ダイヤモンドプリンセス下船開始
2/21 [2.1]
2/26 全国的イベント自粛(Perfume EXILE)
2/29 [1.1]
3/01 ダイヤモンドプリンセス全員下船
2/28 北海道知事の緊急事態宣言
3/02 要請に基づく全国学校休業(-春休み)
3/05 [1.0]
3/08 大相撲無観客場所初日
3/13 [2.1]
3/14 新型インフルエンザ等対策特別措置法改正
3/17 特措法にもとづく新型コロナウイルス感染症対策本部へ
3/20 [1.7]
3/24 東京五輪を2021年に延期
3/25 東京都重要局面発言/春休み
3/28 [1.5]
3/29 志村けん
3/31 [1.0]
4/05 [1.0]
4/07 7都府県に特措法による緊急事態宣言(-5/6)
4/16 [0.5]
4/16 全国に特措法による緊急事態宣言(-5/6)
5/04 全国の緊急事態宣言延長(-5/31)
- - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
細かいところまで対応させて解釈するのはきびしいかもしれない。
[1]新型コロナウイルス(COVID-19)への正しい理解をするためのオンライン学習教材について(島根県立出雲高等学校,大日康史・菅原民枝)
[1]新型コロナウイルス(COVID-19)への正しい理解をするためのオンライン学習教材について(島根県立出雲高等学校,大日康史・菅原民枝)
2020年5月3日日曜日
自分で計算できる実効再生産数
新型コロナウイルス感染症専門家会議が5月1日に出した提言・状況分析における実効再生産数のグラフについてあれこれいわれている。こういう場合は自分で確かめておよその感じをつかみたい。いやいやこんな緊急事態に素人が世情を惑わせるよけいな計算をしてはいけないという声も,かつてよけいなことをしまくったその分野の素人(別の分野の専門家)から聞こえてくるのである。ここでComputational Thinkingを標榜するのであれば,計算の自由(Freedom of Computation)を宣言しておきたい。もちろんそのためには最低限データとアルゴリズムを明らかにしておく必要がある(専門家会議はそうしていない)。
①使用するデータ:日本の新規感染数の日次統計(WHOに報告されたもの)WHOのSituation Reportsのデータ(確定感染者数 Confirmed)は次のようになった。ただし,2月22日から5月1日まで(WHOが公表している日付を基準としたもの)の70点のデータである。
{12,27,12,13,7,22,24,20,9,15,14,16,33,32,59,48,33,26,54,52,55,41,64,34,15,15,44,77,46,50,43,39,65,98,96,112,194,173,87,225,206,233,303,351,383,252,351,511,579,658,743,507,390,455,482,585,628,566,390,367,378,423,469,441,353,203,191,276,236,193}
②使用するモデル:単純なSIRモデルを仮定し,感染が人口の数%を越えて拡がっていないものとし,未感染者数(感受性保持者 Susceptible $S(t)$)が全人口($N$ 定数)とほぼ等しいとする。なお,感染者(Infected $I(t)$)と未感染者の接触による1人1日当りの感染率 $\beta$は対策効果を含めて時間の関数$\beta(t)$とした。さらに,感染期間(日)を$\alpha$として,実効再生産数を$R_t=\alpha \beta(t)$で定義する。このとき,感染者数$I(t)$は次の微分方程式を満足し,$R_t$は$I(t)$とその時間微分から求まる。
\begin{equation}
\begin{aligned}
\dfrac{d I(t) }{dt} = \beta(t) S(t) I(t) / N - I(t) / \alpha \approx \dfrac{ R_t - 1}{ \alpha} I(t) \\
\therefore R_t = 1 + \alpha \dfrac{d I(t) }{dt} / I(t)
\end{aligned}
\end{equation}
③計算方法:誤差はあるけれど時間の単位を1日とする差分式に直して,エクセルで計算する。もとの新規感染数データのままではゆらぎが大きいので,5日移動平均を求めて$I(t)$とする。これから中心差分($I(t+1)-I(t-1))/2$)で1日当りの新規感染数の変化分を求める。さらに,このゆらぎを緩和するためにこの5日移動平均をもとめて$d I(t)$とする。これから②の式を用いて$R_t$を求めた。
④結果:図のとおりである。
[3]感染症数理モデル(北海道大学医学統計学教室のSqquential SEIRモデル)
[4]Rt-COVID-19 Japan (都道府県別新型コロナウイルスの実効再生産数)
[5]山中伸弥による新型コロナウイルス情報発信
[6]A New Framework and Software to Estimate Time-Varying Reproduction Numbers During Epidemics(Cori et al.)
[7]新型コロナ対策専門家会議が判断の拠り所にしている『実効再生産数・倍加時間』の算出方法に関する考察(@makirin1230 2020.05.06)
①使用するデータ:日本の新規感染数の日次統計(WHOに報告されたもの)WHOのSituation Reportsのデータ(確定感染者数 Confirmed)は次のようになった。ただし,2月22日から5月1日まで(WHOが公表している日付を基準としたもの)の70点のデータである。
{12,27,12,13,7,22,24,20,9,15,14,16,33,32,59,48,33,26,54,52,55,41,64,34,15,15,44,77,46,50,43,39,65,98,96,112,194,173,87,225,206,233,303,351,383,252,351,511,579,658,743,507,390,455,482,585,628,566,390,367,378,423,469,441,353,203,191,276,236,193}
②使用するモデル:単純なSIRモデルを仮定し,感染が人口の数%を越えて拡がっていないものとし,未感染者数(感受性保持者 Susceptible $S(t)$)が全人口($N$ 定数)とほぼ等しいとする。なお,感染者(Infected $I(t)$)と未感染者の接触による1人1日当りの感染率 $\beta$は対策効果を含めて時間の関数$\beta(t)$とした。さらに,感染期間(日)を$\alpha$として,実効再生産数を$R_t=\alpha \beta(t)$で定義する。このとき,感染者数$I(t)$は次の微分方程式を満足し,$R_t$は$I(t)$とその時間微分から求まる。
\begin{equation}
\begin{aligned}
\dfrac{d I(t) }{dt} = \beta(t) S(t) I(t) / N - I(t) / \alpha \approx \dfrac{ R_t - 1}{ \alpha} I(t) \\
\therefore R_t = 1 + \alpha \dfrac{d I(t) }{dt} / I(t)
\end{aligned}
\end{equation}
③計算方法:誤差はあるけれど時間の単位を1日とする差分式に直して,エクセルで計算する。もとの新規感染数データのままではゆらぎが大きいので,5日移動平均を求めて$I(t)$とする。これから中心差分($I(t+1)-I(t-1))/2$)で1日当りの新規感染数の変化分を求める。さらに,このゆらぎを緩和するためにこの5日移動平均をもとめて$d I(t)$とする。これから②の式を用いて$R_t$を求めた。
④結果:図のとおりである。
図1 全国の新規感染数の推移(2/22-5/1)
図2 全国の実効再生産数の推移(2/24-4/29)
図2には社会的な事象を書き加えているが,WHOへの報告公表時点とは時間的なずれ(1週間〜10日)があることに注意する。→(注)12日ぐらいか(P. S. 参照)
⑤ 結論:1ヶ月前に1.5〜2.0近くまであった$R_t$が現在0.5〜1.0の範囲にまで落ちてきたことがみてとれ,これは専門家会議の結果とおおよそ近いものである。しかし,細かく見ればそのピークの位置や高さは異なっている。とくに,2月末から3月中旬までの結果は待ったく違う。そもそも出発点となる新規感染数のデータもWHOに報告されたものは,1週間の大きな周期構造を持っており,牧野さんのいうように(ちょっと意味が違うかもしれないけれど),専門家会議が確定感染者数(Confirmed)からどのように処理して新規感染数の推定値を導いているのかがはっきりしないのでもやもやが残る。
P. S. 高橋健太郎さん(@kentarotakahash)によれば,「潜伏期間+発症〜報告までの日数の平均を12日と考えてみたら、かなり納得できました。15日目あたりから一度、下降してRe=1を切りますが、2/24+15-12ですので、2月27日の休校要請の効果に見えます。その下降のピークは3月4日頃。一週間で緩んで、再び上昇が始まった。3月10日頃にRe=2を越えるピーク。」だそうだ。またさらに,「その後、Re=1.5以上の状態が続きますが、三連休の人手の反省があり、3月25日の都知事緊急記者会見を経て、3月27日頃から下降に転じる。3月31日にはRe=1を切り、専門家会議の4月1日には1を下回ったという分析と合致します。」
そして,「その後一度、上昇して、1を越えますが、4月5日頃から本格的な下降が始まる。これは緊急事態宣言が出るというムードの先取り。が、4月14日あたりから再び上昇の兆しというところでしょうか。」なるほどなのだった。
[1]新型コロナウイルス感染症対策専門家会議の見解等(牧野淳一郎,2020.04.18)
[2]新型コロナウイルス感染症対策専門家会議の見解等その2(牧野淳一郎,2020.05.12)[3]感染症数理モデル(北海道大学医学統計学教室のSqquential SEIRモデル)
[4]Rt-COVID-19 Japan (都道府県別新型コロナウイルスの実効再生産数)
[5]山中伸弥による新型コロナウイルス情報発信
[6]A New Framework and Software to Estimate Time-Varying Reproduction Numbers During Epidemics(Cori et al.)
[7]新型コロナ対策専門家会議が判断の拠り所にしている『実効再生産数・倍加時間』の算出方法に関する考察(@makirin1230 2020.05.06)
2020年5月2日土曜日
WHOのSituation reports
WHOがCOVID-19の特設ページで毎日掲載しているSituation reportsの様式が,5月1日版から模様替えした。なんでもいいからCSVで出してほしい。日本の厚生労働省とかわらないのか。
これまでは,もとのpdfファイルから,pdftotext(コマンドラインツール)でテキストにしたものと, PDFelement6 Pro(無料版)でエクセル化したものとを組み合わせて,国・地域別データを整理した日次統計テキストファイルをつくっていた。
新しい様式ではpdftotextの出力がちょっとましな感じだったので,perlプログラミング1発+若干の手作業による修正で,上記の日次統計テキストファイルまでたどり着くことができそうだ。
いや,Johns Hopkins 大学のCSVデータを使えという話もあるかもしれないが,いちおうそこはほれ,WHOを支持しているので。
あいかわらず正規表現もまともに習得していないので泥臭いperlプログラムになった。
- - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
- - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
※WHOのデータ形式が変わったので,若干修正した(2020.5.7)。
これまでは,もとのpdfファイルから,pdftotext(コマンドラインツール)でテキストにしたものと, PDFelement6 Pro(無料版)でエクセル化したものとを組み合わせて,国・地域別データを整理した日次統計テキストファイルをつくっていた。
新しい様式ではpdftotextの出力がちょっとましな感じだったので,perlプログラミング1発+若干の手作業による修正で,上記の日次統計テキストファイルまでたどり着くことができそうだ。
いや,Johns Hopkins 大学のCSVデータを使えという話もあるかもしれないが,いちおうそこはほれ,WHOを支持しているので。
あいかわらず正規表現もまともに習得していないので泥臭いperlプログラムになった。
- - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
# /usr/local/bin/perl
# 05/02/2020 K. Koshigiri
# 05/07/2020 K. Koshigiri -> revised version
# 05/07/2020 K. Koshigiri -> revised version
# extract data from WHO covid-19 reports
# https://www.who.int/emergencies/diseases/
# novel-coronavirus-2019/situation-reports/
# usage:: ./who.pl < pdf-in.txt > out.txt
while($line = <STDIN>) {
chomp($line);
if($line =~ /([A-Z].*)/) {
$a=$1;
$a =~ s/\(.*//;
$flg='a';
} elsif($flg eq 'a' && $line =~ /([\d\h]+)/) {
$b=$1;
$b =~ s/\h//;
$flg='b';
} elsif($flg eq 'b' && $line =~ /([\d\h]+)/) {
$c=$1;
$c =~ s/\h//;
$flg='c';
} elsif($flg eq 'c' && $line =~ /([\d\h]+)/) {
$d=$1;
$d =~ s/\h//;
$flg='d';
} elsif($flg eq 'd' && $line =~ /([\d\h]+)/) {
$e=$1;
$e =~ s/\h//;
$flg='';
print("$a\n$b\n$c\n$d\n$e\n");
}
}
※WHOのデータ形式が変わったので,若干修正した(2020.5.7)。
2020年5月1日金曜日
実効再生産数
新型コロナウイルス感染症対策専門家会議が5月1日の発表で実効再生産数$R_t$の値を示していた。だいぶ前に東京で$R_t$=1.7という数字を出して以来,この値については沈黙していたので,あちこちから不満があがっていたためかもしれない。
図 全国の実効再生産数の値(朝日新聞から引用)
新規感染数のピークが600人を越えていないのは何故だろう。生データや簡単な移動平均では600人を越えると思う。また,推定感染者数となってため,減少期の振動構造も消えているのだろうか。
2020年4月30日木曜日
新規感染数の推移
5月6日が期限であった全国の緊急事態宣言が1ヶ月程度延長されそうであまり異論はないようにみえる。twitterで各国の新規感染数を比較しながらこの問題を検討している人がいた。自分でもやってみた。ただし時間軸は揃え,イタリア,英国,日本×5,スウェーデン×5を試しにやってみる。
図 新規感染数の推移(3/12-4/29)(日本とスウェーデンは5倍した値)
日本のデータが信頼性に欠けているということはさんざん指摘されている。それでもなお日本は,英国の高止まりやスウェーデンの上昇傾向とは異なりイタリアのような下降線に近いようにみえてしまう。本当のところはどうなのだろうか。まだ予断を許さない。
2020年4月29日水曜日
9月入学
どうやら5月6日に緊急事態宣言を解除するのは難しいとわかってきて,目くらましと先延ばしと人気取りのために9月入学を声高に叫び始める維新や国民民主や首長たち。下手すると経産官邸族に唆されてアベノマスク氏も乗ってしまうのかもしれない。やめたほうがいいような気がするけど。やっぱり入学式には桜がないといけませんね。COVID-19の次の波がきたらまた半年づつずらすのかよ。東大が失敗した大学だけシフトはありうるとは思うけれど・・・。子どもたちの学習保障はそれはそれで別に考えるほうがよいと思う。このたいへんで不確定要因が多い時期に更なる混乱を招くだけだろう。むしろ,各大学が入試問題を従来のように作れるのか,大学院入試ができるのか,などが老婆心ながら気になるところ。
2020年4月28日火曜日
東京タワーとスカイツリー
テレビで(テレビの見過ぎ),東京タワーと東京スカイツリーが同じ高さにみえる場所を探すというのがあった。その場所を結ぶ軌跡は円になっていた。そうなのか。
原点に高さ$h_1$の塔を置き,$x=a\ (a>0)$の点に高さ$h_2\ (>h_1)$の塔を置く。$x$軸上には仰角が等しくなる点が2つあり,$x/h_1 = (a-x)/h_2$と$x/h_1 = (a+x)/h_2$を満たす点であり,$x=\frac{a}{1 \pm h_2/h_1}$ で与えられる。
次に点P $(x,y)$を考えて,この点からの仰角が等しくなるための条件を求めれば,
\begin{equation}
\dfrac{x^2+y^2}{h_1^2} = \dfrac{(a-x)^2+y^2}{h_2^2}
\end{equation}
である。整理すれば以下のように円の方程式が得られる。ここで,無次元の量 $c$を $c=(h_2/h_1)^2-1$と置いた。
\begin{equation}
\begin{aligned}
\bigl\{ ( h_2 / h_1 )^2 - 1 \bigr\} x^2 + 2 a x + \bigl\{ ( h_2 / h_1 )^2 - 1 \bigr\} y^2 = a^2 \\
(x + a/c)^2+y^2=a^2/c *\bigl( 1 + 1/c \bigr) = (a/c * h_2/h_1)^2
\end{aligned}
\end{equation}
中心の位置は先ほど$x$軸上に求めた2点の中点になっている。円の半径は$a/c * h_2/h_1$である。
原点に高さ$h_1$の塔を置き,$x=a\ (a>0)$の点に高さ$h_2\ (>h_1)$の塔を置く。$x$軸上には仰角が等しくなる点が2つあり,$x/h_1 = (a-x)/h_2$と$x/h_1 = (a+x)/h_2$を満たす点であり,$x=\frac{a}{1 \pm h_2/h_1}$ で与えられる。
次に点P $(x,y)$を考えて,この点からの仰角が等しくなるための条件を求めれば,
\begin{equation}
\dfrac{x^2+y^2}{h_1^2} = \dfrac{(a-x)^2+y^2}{h_2^2}
\end{equation}
である。整理すれば以下のように円の方程式が得られる。ここで,無次元の量 $c$を $c=(h_2/h_1)^2-1$と置いた。
\begin{equation}
\begin{aligned}
\bigl\{ ( h_2 / h_1 )^2 - 1 \bigr\} x^2 + 2 a x + \bigl\{ ( h_2 / h_1 )^2 - 1 \bigr\} y^2 = a^2 \\
(x + a/c)^2+y^2=a^2/c *\bigl( 1 + 1/c \bigr) = (a/c * h_2/h_1)^2
\end{aligned}
\end{equation}
中心の位置は先ほど$x$軸上に求めた2点の中点になっている。円の半径は$a/c * h_2/h_1$である。
2020年4月27日月曜日
有界な単調数列は収束する
大人の学び直し
- - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
○実数を項とする無限数列 $\{a_n\}$ を考える。すなわち,$n \in \mathbb{N}$,$a_n \in \mathbb{R}$ である。数列 $\{a_n\}$ の全ての項を要素とする集合を $A$ とする。すなわち,$A=\{a_1, a_2, a_3, \dots \}$ である。
○集合 $X$ が 上に(下に)有界 であるとは,$\forall x \in X \rightarrow x \le (\ge) M$ となる実数 $M$ が存在することである。この $M$ を $X$ の上界(下界) とよぶ。$X$ が上にも下にも有界であれば,$X$ は 有界 であるという。
○上界(下界)$M$ が $M\in X$ であるとき,これを $X$ の 最大値(最小値) という。
○上界(下界)の集合が空集合 $\emptyset$ でないとき,上界(下界)の最小値を $X$ の上限(下限) という。空集合ならば,上限(下限)を $\infty \ (-\infty)\ $ と表すことがある。
○なお,数列 $\{a_n\}$ については,その全ての項からなる集合 $A$ についての表現を流用して,数列に対して,有界,上界(下界),最大値(最小値),上限(下限)などの用語をあてはめることにする。
○数列 $\{a_n\}$ が有界ならば,$\forall n \in \mathbb{N} \rightarrow |a_n| \le M$ と表すことができる。
○数列 $\{a_n\}$ が 単調増加(減少) であるとは,すべての$n \in \mathbb{N}$に対して,$a_n \le a_{n+1}\ ( a_n \ge a_{n+1} )\ $ が成立することである。等号を含めない場合は, 狭義単調増加(減少) であるという。単調増加と単調減少の性質を持つ数列をまとめて 単調数列 という。
○数列が収束する ことは次のように表現する。各項が実数である無限数列 $\{a_n\}$ がある。この数列が実数 $\alpha$ に収束するとは,つぎの関係が成り立つことをいう。『任意の $\varepsilon > 0$ に対して,ある自然数 $N(\varepsilon)$ が存在して,$n \ge N(\varepsilon)$ をみたす 任意の自然数 $n$ について $| a_n - \alpha | < \varepsilon $をみたす』
$\forall \varepsilon > 0,\ \exists N(\varepsilon) \in \mathbb {N} \ \mathrm{s.t.}\ \forall n \in \mathbb {N} \quad [\ n \ge N(\varepsilon) \Rightarrow | a_{n} - \alpha | < \varepsilon \ ]$
○「 有界な単調数列は収束する 」を証明するための前提としては,実数に関する次の公理が必要となる。すなわち,「上に(下に)有界な実数の部分集合には最小上界(最大下界)が存在する。」
○証明は次のように進む。上に(下に)有界な数列 $\{a_n\}$ があるとすると,その最小上界(最大下界)を $\alpha$ とすると,すべての $n$ に対して,$a_n \le \alpha \ (a_n \ge \alpha)\ $ が成り立つ。
○ 最小上界より小さな数(最大下界より大きな数) $\alpha \mp \varepsilon \ ( \varepsilon > 0 )\ $を考えると,この数と $\alpha$ との間には数列 $\{a_n\}$ の部分が存在する(存在しなければ, $\alpha$ が最小上界や最大下界ではないことになるから)。つまり,$\varepsilon$ を与えると定まる自然数 $N$ が存在し,それは,$a_N > \alpha -\varepsilon \ ( a_N < \alpha + \varepsilon )\ $を満足する。
○$\{a_n\}$ は単調増加(単調減少)数列なので,$n \ge N$ となる $n$ に対して,$a_n \ge a_N > \alpha -\varepsilon \ (a_n \le a_N < \alpha + \varepsilon)\ $である。一方,$a_n \le \alpha \ ( a_n \ge \alpha )\ $ より,$a_n < \alpha + \varepsilon \ (a_n > \alpha - \varepsilon )\ $ である。
○これらより,$n \ge N$ となるすべての $n$ に対して,$ |a_n - \alpha | < \varepsilon $ が成り立つ。したがって,数列 $\{a_n\}$ は $\alpha$ に収束する。これを次式のように表して,$\alpha$ を収束する数列の 極限値 という。
$\lim_{n \to \infty} a_n = \alpha$
2020年4月26日日曜日
COVID-19雑感(2)
昨日のものを再編してみた。
○ニューヨーク州の抗体検査による既感染累計が人口の14%というのはほんとうだろうか。
(もしそうならモデルパラメタの前提がそもそも間違っている)
○スウェーデンの試み(ロックダウンしない)は成功するのだろうか。死亡数累計が人口の0.02%を越えて増加中である。スペインの0.04%よりは小さいが,増加率が・・・
○ブラジル,ロシアなどもじわじわと増えている。
○ニューヨーク州の抗体検査による既感染累計が人口の14%というのはほんとうだろうか。
(もしそうならモデルパラメタの前提がそもそも間違っている)
○スウェーデンの試み(ロックダウンしない)は成功するのだろうか。死亡数累計が人口の0.02%を越えて増加中である。スペインの0.04%よりは小さいが,増加率が・・・
○ブラジル,ロシアなどもじわじわと増えている。
図 欧州・米州の新規感染数累計の推移(人口の10ppm時点を原点)
2020年4月25日土曜日
COVID-19雑感(1)
徒然なるままに・・・
○日本は相変わらず情緒的な対処法で乗り切ろうとしている。正確なデータがないままに。
○シンガポールの新規感染数累計は,人口比で0.2%となり湖北省の0.1%を越えた。まだ収まる様子がみえないのだけれど大丈夫かしら(それにしては死亡数累計が少ない)。
○東京は,韓国・オーストラリアを越えてまだ収束先がみえない。日本全体も上昇中。
(残念なことに,石川県と福井県が人口比で東京についで2位と3位なのだ)
○台湾,中国,韓国,香港は,第1段階が終息している。
○通常のインフルエンザと比較して問題なしとする正論?は正しいのだろうか。
○日本は相変わらず情緒的な対処法で乗り切ろうとしている。正確なデータがないままに。
○シンガポールの新規感染数累計は,人口比で0.2%となり湖北省の0.1%を越えた。まだ収まる様子がみえないのだけれど大丈夫かしら(それにしては死亡数累計が少ない)。
○東京は,韓国・オーストラリアを越えてまだ収束先がみえない。日本全体も上昇中。
(残念なことに,石川県と福井県が人口比で東京についで2位と3位なのだ)
○台湾,中国,韓国,香港は,第1段階が終息している。
○通常のインフルエンザと比較して問題なしとする正論?は正しいのだろうか。
図 アジア・太平洋の新規感染数累計の推移(人口の10ppm時点を原点)
登録:
投稿 (Atom)