リザーバー・コンピューティング

脳オルガノイド計算からの続き

これは，リザーバー・コンピューティングについて，Bardに聞いてChatGPTに和訳してもらった解説だ。質問者（自分）のスペルが reserverと間違っていたけれど，修正して答えてくれた。このレベルになると，どの程度フェイク成分があるのかが判別できない。

Ｑ：Please explain about reservoir computing.

Ａ：Bard + ChatGPT

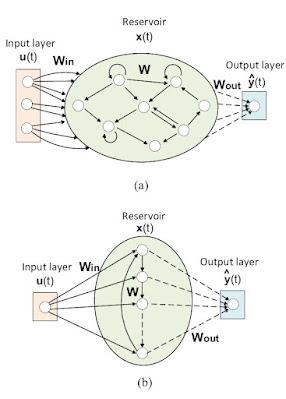
Reservoir computing（リザーバーコンピューティング）は、再帰ニューラルネットワークに着想を得た比較的新しい計算フレームワークです。この手法は、入力信号をリザーバーと呼ばれる固定された非線形システムのダイナミクスを使用して、高次元の計算空間にマッピングすることによって機能します。このリザーバーは、水のバケツや回路などの物理的なシステムであるか、微分方程式の系などの数学的なモデルであることができます。

その後、リザーバーの出力は線形の読み出し関数を使用して読み取られます。この読み出し関数は、リザーバーの状態と所望の出力との関係を学習するためにトレーニングできます。

図：リザーバーコンピューティングアーキテクチャ

（編者注： Rossello (2018)の図 [1] へ勝手にリンク引用しているBard）

リザーバーコンピューティングの利点の一つは、非常に効率的であることです。リザーバーは非常に単純であり、読み出し関数は比較的単純で速いアルゴリズムである線形回帰を使用して学習できます。これにより、低消費電力とリアルタイムのパフォーマンスが重要なアプリケーションに適しています。

リザーバーコンピューティングのもう一つの利点は、非常に柔軟であることです。同じリザーバーは、読み出し関数を変更するだけでさまざまなタスクを学習するのに使用できます。これにより、タスクが事前にはわからない場合や、タスクが時間とともに変化する場合に適しています。

リザーバーコンピューティングはまだ比較的新しい分野ですが、計算の仕方を革新する可能性があります。既に音声認識、画像認識、およびロボット制御など、さまざまなアプリケーションで使用されています。

以下はリザーバーコンピューティングに関するいくつかの追加の詳細です：

　・リザーバーは通常、多くの内部状態を持つ高次元システムです。これらの状態は複雑な方法で相互作用し、リザーバーが非線形関数を計算できるようにします。

　・読み出し関数は通常、リザーバーの状態の線形関数です。この関数は、所望の入出力関係の例などのトレーニングデータを使用して学習できます。

　・リザーバーコンピューティングは、サポートベクターマシンやディープラーニングなどの他の機械学習技術と組み合わせて使用されることがよくあります。これにより、システムの精度とパフォーマンスを向上させるのに役立ちます。

Bard, Perplexity, Bing などは正確性を若干担保するために実在して関係あるURLへのリンクを提供しているが，それを埋め込み図の形で提供するのを見たのは初めてかもしれない。

以下は真正の参考文献：

［１］Simple Cyclic Reservoir Computing with FPGA Devices for Efficient Channel Equalization

［２］A Survey on Reservoir Computing and Its Interdisciplinary Applications Beyond Traditional Machine Learning（2023, H. Zhang and D. V. Vargas）

脳オルガノイド計算

数日前，インディアナ大学のチームが，ヒト脳幹細胞から作成した脳オルガノイドをコンピュータ・チップに取り付けてAIツールに接続したシステム（Brainoware）で，初歩的な音声認識を含む，情報処理・学習・記憶ができることを実証したとのニュースが流れた。

ちょうど，しばらく前のNHKのフロンティア第２回「AI 究極の知能への挑戦」でも，脳を利用した計算チップの話が取り上げられていた。東大の池内与志穂准教授のグループが16点のプローブ上においた脳オルガノイドを２つ接続して，反応を観察する様子や，オーストラリアのBrett Kaganのグループの実験室の詳細な映像を見ることができた。

Kaganは，1970年代の最初期のコンピュータゲーム（アーケードゲーム）であるPON（ピンポンゲーム）をこの脳オルガノイドシステムにやらせていて，学習効率の高さを強調していた。すごくないか。

写真：脳オルガノイドチップ（左 F. Guo et. al. から，右 B. Kagan et. al. から引用）

［１］ Brain organoid reservoir computing for artificial intelligence（Feng Guo et. al.）

［２］‘Biocomputer’ combines lab-grown brain tissue with electronic hardware（Nature）

［３］脳オルガノイドをコンピューターに接続，日本語の音声認識に成功（MIT Tech Review）

［４］In vitro neurons learn and exhibit sentience when embodied in a simulated game-world（B. Kagan et. al.）

［５］Cortical Labs（https://spikestream.corticallabs.com/）

折り紙で３次方程式（２）

折り紙で３次方程式（１）からの続き

Mathematicaで折り紙の3次方程式問題をplotする関数を書いてみた。

最初に，Plot[{-x - 3, x + 1, 2 x, (x + 2)^2/4,   Sqrt[8 (x)] - 1, -Sqrt[8 (x)] - 1}, {x, -8, 8},  AspectRatio -> Automatic, PlotRange -> {-8, 8}]　こんな風に問題ごとにプロットしてみた。係数を混同していてなかなか正解にたどりつかなかったが，どうにか安定して答えがでてきた。ただし，接線の方程式は目の子であてはめている。

係数，a,b,c,dを与えて，焦点，準線，放物線，接線をすべて描画するように改善したものが次のコードである。最終ステップで，三次方程式を解いた解が3つリストとして出てくるので，これを実数の個数によって場合分けして描画するのはさぞ面倒だろうと心配していたのだが，リストの成分表示からリストに直しただけで求めていた結果が得られてしまった。虚数解が入ってきても何の問題もなくスキップしてくれた。やはりMathematicaは賢い。

そのコードは次のようなものである。

fold3[a_, b_, c_, d_] := 

{g0 = Graphics[{Point[{b, a}], Point[{d, c}], 

      Line[{{-10, -a}, {10, -a}}], Line[{{-d, -10}, {-d, 10}}]}, 

     Axes -> True]; 

 g1 = Plot[{(x - b)^2/(4*a), Sqrt[4 d x] + c, -Sqrt[4 d x] + c},

    {x, -10, 10}, PlotRange -> {-10, 10}, AspectRatio -> Automatic]; 

 sol = Solve[a t^3 + b t^2 + c t + d == 0, t]; 

 t1 = t /. sol; 

 s1 = -( a t1*t1 + b t1);

 g2 = Plot[t1 x + s1, {x, -10, 10}, PlotRange -> {-10, 10}, 

     AspectRatio -> Automatic, PlotStyle -> Red];

 Show[g0, g1, g2]}[[1]]

この関数で，fold3[1, 2, -2, -1]，fold3[1, 1, 1, 1]，fold3[1, 0, -1, 0.0001] を実行した結果を以下に示す。傾きが0の場合は，極限値として得られることになる。

図：fold3の実行結果

折り紙で３次方程式（１）

代数学の基本定理とガロアのおかげなのかどうかは知らないけれど，5次方程式を代数的に解くための一般公式はないことは誰もがみんな知っている。知らんけど。

(1) 放物線の性質

・放物線$\mathcal{L}$の焦点Fが $\ (b,a)\ $，準線$\ \ell\ $が $\ y=-a\ $のとき，この放物線を$\mathcal{L}(b,a:y)$と書く。例えば，$\mathcal{L}(d,c:x)$ならば，焦点が$\ (d,c)\ $で，準線の式は $\ x=-d\ $になる。

・放物線$\mathcal{L}(b,a:y)$上の点Pを$\ (x,y)\ $とすると，距離FP=$\sqrt{(x-b)^2+(y-a)^2}\ $と，点Pから準線に下ろした垂線の足Hへの距離 PH=$y+a\ $が等しいという性質がある。

・$\mathcal{L}(b,a:y)$の式は，$y=(x-b)^2/4a$，$\mathcal{L}(d,c:x)$の式は，$x=(y-c)^2/4d\ $となる。

(2) 折り紙で放物線の接線を折る

・折り紙上に直交直線座標系をとって，焦点Fと準線$\ \ell\ $を記す。

・準線$\ \ell\ $が焦点Fに重なるように折り紙を折線$\ f\ $で折ると，$\ell\ $上にFの像Gができる。

・折り紙を広げるとFGの中点Qは放物線$\mathcal{L}$上の点であり，かつ折線$\ f\ $上の点になる。

・$f\ $はQを接点とする$\mathcal{L}$の接線となる。また，$f\ $の集合の包絡線が$\mathcal{L}$である。

(3) ３次方程式との関係

・折り紙上に２つの放物線，$\mathcal{L}(b,a:y)$と$\mathcal{L}(d,c:x)$を考える。

・その共通の接線となる折線$\ f\ $が少なくとも1つ（あるいは最大の3つ）存在する。

・折り紙上の直交直線座標系で，折線$\ f\ $が$\ y=t x + s\ $となるとき，傾き$\ t\ $が

2放物線の焦点の座標からなる3次方程式$\ a t^3+b t^2 + c t + d = 0\ $の解に対応する。

(4) その説明

接点の座標をQ$\ (\beta,\alpha)\ $として，$\mathcal{L}(b,a:y)$に接する折線の方程式を考えると，

$y-\alpha = (\beta -b)/2a \cdot (x -\beta)\ $であり，$\alpha = (\beta -b)^2/4a\ $が成り立つ。

$\therefore y = (\beta -b)/2a \cdot x -(\beta -b)(\beta + b)/4a = t x + s$，

$\ \beta\ $を消去して，$s = -(a t^2 + 2 b t)\cdots$①

次に，接点の座標をR$\ (\delta,\gamma)\ $として，$\mathcal{L}(d,c:x)$に接する折線の方程式を考えると，

$x-\delta = (\gamma -c)/2d \cdot (y -\gamma)\ $であり，$\delta = (\gamma -c)^2/4d\ $が成り立つ。

$\therefore x = (\gamma -c)/2d \cdot y -(\gamma -c)(\gamma + c)/4d = y / t  - s / t $，

$\ \gamma\ $を消去して，$s=c + d/t\cdots$②

①②より，$\bm{a t^3+b t^2 + c t + d = 0}$ が導かれた。

［１］折り紙の中の数学（三谷純）

［２］代数方程式の折り紙による解法について（森継修一，中村怜子）

［３］折り紙による五次方程式の解法（西村保三，山本一海）

［４］折り紙の数学（上越教育大学公開講座）

［５］Geometric solution of a quintic equation by two-fold origami（J. C. Lucero）

Π角形

YouTubeでm/n角形という話題を見かけた。

これは，タートルグラフィックスの定番らしい。Processingでプログラムを作ってみることにする。久々のProcessingはロゴも変わりバージョンは4.1.1になっている。

タートルグラフィックスの見本コードがサンプルの中にあったので，それを参考にしてみる。クリックするとタートルが進むとして，k角形の形は，一辺の長さを進むタートルの進行方向（方向単位ベクトル）の方位角が，進むたびに360度/kづつ増加するものと定義する。

float turtleX;

float turtleY;

float turtleT;

float k;

void setup() {

  size(512, 512);

  turtleX = width/2;

  turtleY = height/2;

  turtleT = 0;

  k=3.1415926;

  background(255);

}

void forward(float go) {

  float newX = turtleX + go*cos(turtleT);

  float newY = turtleY + go*sin(turtleT);

  line(turtleX, turtleY, newX, newY);

  turtleX = newX;

  turtleY = newY;

}

void rotate(float rot) {

  turtleT = turtleT - radians(rot);

}

void mousePressed() {

  strokeWeight(2);

  stroke(mouseX/2,mouseY/2,random(0,255));

  forward(128);

  rotate(360/k);

}

ここではm/nとして簡単な有理数ではなくて，円周率の近似値（有効数字8桁）を与えてみた。つまり，Π角形の作図になる。マウスクリックでタートルが進むようにした上で，線の色はクリック位置と乱数の組み合わせで選ぶことにする。

図：Π角形作図の途中段階のイメージ

２次元ルービック

Twitterで@jagarikinさんが，ルービックキューブの２次元表現のアニメーションに成功していた。さっそくこれををTikzで描いてみた。

図：２次元ルービックの概念図

(1) 3重の円を3個配置する。2つの円のひとかたまりの交点群は，9個の色つきマークの1組として表わされる。こうしてできた6つの組がルービックキューブの6面に対応し，各マークはルービックキューブのピースに該当する。ルービックキューブの回転操作はこの円に沿って，マークを組単位で回転移動することに相当する。

(2) 色つきマークの組の中心マークが6個あり，これがルービックキューブの6個のセンターピースに対応する。これらは相対的な配置が固定された不動点になるので，これを通る破線の円は動かす必要がない。外側の円と内側の円に沿っての回転だけを考えればよい。

(3) 実線でつながる3個のマークが8組あり，これが8個のコーナーピースに対応する。破線でつながる2個のマークが12組あり，これが12個のエッジピースに対応する。

(4) 内側の円に沿った回転操作にともなって，回転操作を行った円に囲まれた9個の組もピースの関係を保持するために同じ向きに回転する。外側の円に沿った回転操作にともなって，回転操作を行った円の外側にある9個の組もピースの関係を保持するために逆向きに回転する必要がある。

フィボナッチ数列と1/89

不思議な式をみかけたのでメモ。小数点以下の数字の並びがフィボナッチ数列になっている有理数のこと。

$ \dfrac{1}{89}  = 0.0112359550... \\ = 0.01 + 0.001 + 0.0002 + 0.00003 + 0.000005 + 0.0000008 + 0.00000013 + ... \\ = \dfrac{1}{10^2} + \dfrac{1}{10^3} + \dfrac{2}{10^4} + \dfrac{3}{10^5}  + \dfrac{5}{10^6} + \dfrac{8}{10^7} + \dfrac{13}{10^8} + ... $

そこで，フィボナッチ数列を$F_i \ (F_0=0，F_1=1， F_2=1， F_{i+1}=F_{i}+F_{i-1}： i\ge1)$として，次の和$S$を定義する。$\displaystyle S = \sum_{i=1}^{\infty} \dfrac{F_i}{10^{i+1}}$

このとき，$\displaystyle S=\sum_{i=1}^{\infty} \dfrac{F_i}{10^{i+1}} = \sum_{i=2}^{\infty} \dfrac{F_{i-1}}{10^i}，10 S = \sum_{i=1}^{\infty} \dfrac{F_i}{10^i}$ である。

$\displaystyle \therefore 100S = \sum_{i=1}^{\infty} \dfrac{F_i}{10^{i-1}} = F_1 + \sum_{i=1}^{\infty} \dfrac{F_{i+1}}{10^i} = F_1 + \sum_{i=1}^{\infty} \dfrac{F_i + F_{i-1}}{10^i}  = F_1 + 10 S + S$

これから $S = \dfrac{1}{89}$がでてくる。

［１］1/89がフィボナッチ数列を表すのはなぜですか？

［２］小数点以下にフィボナッチ数列が出現する有理数

逆順と平方（３）

逆順と平方（２）からの続き

9桁までの範囲で考えるとしても，３億個のデータのうち条件を満足するのが高々7000個なので，ほとんど無駄な計算をしていることになる。そこで，プログラムは汚くとも，もう少し計算を簡略化できないかと考えた結果，12桁までの計算が数分程度で可能になった。2〜3桁分をまとめてループをまわしているが，この範囲でよいという証明はしたわけではなく，直感に頼っているのだった。

function reverse(n,m)
  nun=zeros(Int,m)
  nre=0
  for k in 1:m
    nun[k] = n % 10
    nre = nre + nun[k]*10^(m-k)
    n = div(n - nun[k],10)
  end
  return nre
end

function counter(n)
  a = [0 1 2 3 10 11 12 13 20 21 22 23 30 31 100 101 102 103 110 111 112 113 120 121 122 123 130 131 200 201 202 203 210 211 212 213 220 221 222 223 230 231 300 301 302 303 310 311 312 313]
  b = [50 4 14]
  c = [10^3 10 10^2]
  cnt=1
  kk = c[n%3+1]
  k1max = b[n%3+1]
  k2max = 1 + div(n+10,14)*49
  k3max = 1 + div(n+10,17)*49
  k4max = 1 + div(n+10,20)*49
  for k1 in 1:k1max
    for k2 in 1:k2max
      for k3 in 1:k3max
        for k4 in 1:k4max
          k=a[k1]+a[k2]*kk+a[k3]*kk*10^3+a[k4]*kk*10^6
          if(k!=0)
            m=Int(ceil(log10(k)+10^(-9)))
            kj=BigInt(k)^2
            mj=Int(ceil(log10(kj)+10^(-9)))
            kr=reverse(k,m)
            krj=BigInt(kr)^2
            if(reverse(kj,mj)==krj)
# println(k,":",kr,":",kr^2,":",reverse(k^2,mj))
              cnt=cnt+1
            end
          end
        end
      end
    end
  end
  return cnt
end

for i in 1:12
  @time println(i," : ",counter(i))
end

1 : 4
0.000491 seconds (176 allocations: 6.000 KiB)
2 : 13
0.000551 seconds (765 allocations: 22.258 KiB)
3 : 37
0.002469 seconds (3.68 k allocations: 96.281 KiB)
4 : 100
0.005823 seconds (18.99 k allocations: 466.195 KiB)
5 : 253
0.021409 seconds (81.69 k allocations: 1.886 MiB)
6 : 615
0.091992 seconds (346.74 k allocations: 7.780 MiB)
7 : 1434
0.441439 seconds (1.61 M allocations: 35.324 MiB, 11.21% gc time)
8 : 3244
1.616126 seconds (6.39 M allocations: 138.140 MiB, 11.31% gc time)
9 : 7116
6.780644 seconds (25.58 M allocations: 546.322 MiB, 13.04% gc time)
10 : 15200
28.310428 seconds (113.32 M allocations: 2.337 GiB, 13.25% gc time)
11 : 23284
108.389549 seconds (437.13 M allocations: 8.934 GiB, 13.71% gc time)
12 : 31368
417.966111 seconds (1.71 G allocations: 34.604 GiB, 14.30% gc time)

逆順と平方（２）

逆順と平方（１）からの続き

中嶋慧さんのpythonによる逆順関数がスマートだったので Juliaでも試してみた。数値を文字列に変換して，逆順にしたものをもういちど数値に戻すというものだ。プログラムとしてはスッキリしたけれど，実行時間が倍になってしまった。

function rev(n)
  b = string(n)
  c = b[end:-1:1]
  d = parse(Int,c)
  return d
end

function counter(m,j)
  cnt = 1
  kmax = Int(ceil(10^(m-1)*sqrt(10)))
  for k in 10^(m-1)+1:kmax
    kr = rev(k)
# kj = BigInt(k)^j
# krj = BigInt(kr)^j
    kj = k*k
    krj = kr*kr
    if(rev(kj)==krj)
# if(2000<=k<=2299)
# println(k,":",kr,":",kr^j,":",rev(k^j))
# end
      cnt = cnt + 1
    end
  end
  return cnt
end

function list(l,j)
  sum=1
  for i in 1:l
    @time sum = sum + counter(i,j)
    println(i," **",j," = ",sum)
  end
end

list(9,2)
0.000010 seconds (36 allocations: 1.781 KiB)
1 **2 = 4
0.000015 seconds (264 allocations: 13.062 KiB)
2 **2 = 13
0.000138 seconds (2.60 k allocations: 128.844 KiB)
3 **2 = 37
0.001734 seconds (25.96 k allocations: 1.254 MiB)
4 **2 = 100
0.016847 seconds (259.48 k allocations: 12.538 MiB)
5 **2 = 253
0.224788 seconds (2.59 M allocations: 125.376 MiB, 12.69% gc time)
6 **2 = 615
2.393325 seconds (25.95 M allocations: 1.224 GiB, 12.89% gc time)
7 **2 = 1434
26.113517 seconds (259.47 M allocations: 12.244 GiB, 11.55% gc time)
8 **2 = 3244
284.531202 seconds (2.59 G allocations: 128.882 GiB, 11.40% gc time)
9 **2 = 7116

逆順と平方（１）

 中嶋慧さんが，次のようなプログラムについての話題を提供していた。ある数nの逆順に並べた数をrev(n)とする。例えば，rev(123)は321である。このとき，rev(n^2)=rev(n)^2を満たすm桁の数nは，何個あるかという問題だ。pythonでは時間がかかるので，juliaにするとよいのではないかという提案だったが，残念ながら，工夫に乏しい10^8個の計算はやたら時間を食うだけだった（追伸：条件が rev(rev(k)^2) = k^2 であると誤解していたので，その後訂正したところ，中嶋さんの結果と一致した）。

function reverse(n,m)
  nun = zeros(Int,m)
  nre = 0
  for k in 1:m
    nun[k] = n % 10
    nre = nre + nun[k]*10^(m-k)
    n = div(n - nun[k],10)
  end
  return nre
end

function counter(m)
  cnt = 1
  kmax = Int64(ceil(10^(m-1)*sqrt(10)))

  for k in 10^(m-1)+1:kmax

    kr = reverse(k,m)

    m2 = Int(ceil(log10(k*k)))

    if(reverse(k*k,m2)==kr*kr)

# if(2000<=k<=2299)
# println(k,":",kr,":",kr^2,":",reverse(kr^2,m2),":",k^2)
# end
      cnt = cnt+1
    end
  end
  return cnt
end

function list(l)

  sum = 0
  for i in 1:l
    @time sum = sum + counter(i)

    println(i," : ",sum)
  end

end

list(9)
0.000003 seconds (6 allocations: 576 bytes)
1 : 4
0.000009 seconds (44 allocations: 4.469 KiB)
2 : 13
0.000097 seconds (434 allocations: 50.859 KiB)
3 : 37
0.000901 seconds (4.33 k allocations: 540.750 KiB)
4 : 100
0.011719 seconds (43.25 k allocations: 5.939 MiB)
5 : 253
0.145435 seconds (432.46 k allocations: 62.688 MiB, 12.05% gc time)
6 : 615
1.100731 seconds (4.32 M allocations: 692.869 MiB, 17.40% gc time)
7 : 1434
11.497505 seconds (43.25 M allocations: 7.088 GiB, 16.11% gc time)
8 : 3244
132.445766 seconds (432.46 M allocations: 77.329 GiB, 16.48% gc time)
9 : 7116

レピュニット

レピュニット数（repunit = Repeated Unit ） とは，全ての桁が１である自然数のことである。例えば，１，11，111，1111，11111，111111・・・などである。１が$n$個並ぶレピュニット数を$R_n$と書くと，$R_n = \dfrac{10^n - 1 }{9}$である。

tujimotterの「任意の素数はレピュニットの素因数に現れる（2, 5を除く）あとダイヤル数」によると，次の定理「2と5 を除く任意の素数 $p$ に対し，ある正整数 $n>1$ が存在して $R_n$は p で割り切れる」が成り立つ。このとき，$R_n = \dfrac{10^n - 1 }{9} \equiv 0 ,\quad (\mod\ p)$

$p \neq 3$ならば($R_3 = 111 \equiv 0 \mod 3$なので，$p =3$ は OK)，$10^n \equiv 1 \ (\mod p) , \quad n>1 $が成り立てばよい。これはフェルマーの小定理にほかならない。

フェルマーの小定理：互いに素である整数 $a$ と 素数 $p$ に対し，$a^{p−1} \equiv 1 \ (\mod p)$が成り立つ。

ほとんど正三角形

Twitterでほとんど正三角形にみえる二等辺三角形が話題になっていた。数学パズル作家のポテト一郎さんが，簡単で精度の高いものを考案したのでそれをtikzで描いてみた。話題の発端となったその１は各辺が，$\sqrt{64},\sqrt{65},\sqrt{65}$である。その２が新しく考案されたもので，各辺が$\sqrt{241}/2,\sqrt{241}/2,\sqrt{242}/2$である。

図１　ほとんど正三角形その１

図２　ほとんど正三角形その２

東京タワーとスカイツリー

テレビで（テレビの見過ぎ），東京タワーと東京スカイツリーが同じ高さにみえる場所を探すというのがあった。その場所を結ぶ軌跡は円になっていた。そうなのか。

原点に高さ$h_1$の塔を置き，$x=a\ (a>0)$の点に高さ$h_2\ (>h_1)$の塔を置く。$x$軸上には仰角が等しくなる点が２つあり，$x/h_1 = (a-x)/h_2$と$x/h_1 = (a+x)/h_2$を満たす点であり，$x=\frac{a}{1 \pm h_2/h_1}$ で与えられる。

次に点P $(x,y)$を考えて，この点からの仰角が等しくなるための条件を求めれば，
\begin{equation}
\dfrac{x^2+y^2}{h_1^2} = \dfrac{(a-x)^2+y^2}{h_2^2}
\end{equation}
である。整理すれば以下のように円の方程式が得られる。ここで，無次元の量 $c$を　$c=(h_2/h_1)^2-1$と置いた。
\begin{equation}
\begin{aligned}
\bigl\{ ( h_2 / h_1 )^2 - 1 \bigr\} x^2 + 2 a x + \bigl\{ ( h_2 / h_1 )^2 - 1 \bigr\} y^2 = a^2 \\
(x + a/c)^2+y^2=a^2/c *\bigl( 1 + 1/c \bigr) = (a/c * h_2/h_1)^2
\end{aligned}
\end{equation}
中心の位置は先ほど$x$軸上に求めた２点の中点になっている。円の半径は$a/c * h_2/h_1$である。

立春の問題

今日は立春。暖く晴れた春の一日。

こんな日は数学パズル。これを解くのがComputational Thinkingなのだろうか？
次の四角の中には１〜９の数が１回づずはいる。その配列を求めよ。という問題をtwitterでみかけた。

図　ピーターからの問題？

これを解くためにJuliaを用いると次のようになった。9重の整数のループがあってとてもださい。ループの範囲を集合にして１つずつ減らしていくということも考えられたが，もっときたなくなりそうなのでこれはやめ。それでも取り合えず答えは得られた。和と積で絞るのはちょっとトリッキーなので，正統的ではない。答えは１通りしかないというヒントに基づいている。

- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - 

function loop()

  for i1 in 1:9

    for i2 in i1+1:9

      for i3 in i2+1:9

        for i4 in 1:9

          for i5 in 1:9

            for i6 in 1:9

              for i7 in 1:9

                for i8 in 1:9

                  for i9 in 1:9

                    a=i1+i2+i3+i4+i5+i6+i7+i8+i9

                    b=i1*i2*i3*i4*i5*i6*i7*i8*i9

                    c=i1/(10*i4+i7)+i2/(10*i5+i8)+i3/(10*i6+i9)

                    if a==45 && b==362880 && c==1

                      return (i1,i2,i3,i4,i5,i6,i7,i8,i9)

                    end

                  end

                end

              end

            end

          end

        end

      end

    end

  end

end

- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - 

@time loop()

  0.191865 seconds (201.31 k allocations: 10.933 MiB, 2.17% gc time)

(5, 7, 9, 3, 6, 1, 4, 8, 2)

三角関数と双曲線関数

mathtodonで@Sun_Pillar@mathtod.online（サンピラー）さんが出していた問題をちょっと改変するとこんな感じだった。

$f(x) = \sin x + \csc x + \cos x + \sec x + \tan x + \cot x$ と
$fh(x) = \sinh x + \csch x + \cosh x + \sech x + \tanh x + \coth x$の
極小値は一致することを示せ。ただし，$ 0 < x < \pi/2$とする。

えー，ホントかなと思ったが，数値計算してみると確かにそうだ。その極小値は一瞬 $2\pi = 6.28319$ に見えたが，落ち着いて考えると，ともに，$2+3\sqrt{2}=6.24264$となった（ただし，これを与える$x$の値は，$f(x)$と$fh(x)$では異なる）。

さらに，$f(x)$ では $y = \tan x$とおき，$fh(x)$ では $y=\sinh x$とおくと，

$f(x(y))= \dfrac{y}{\sqrt{1+y^2}} +  \dfrac{\sqrt{1+y^2}}{y} +   \dfrac{1}{\sqrt{1+y^2}} +  \sqrt{1+y^2} + y + \dfrac{1}{y}$

$fh(x(y))= y + \dfrac{1}{y} +   \sqrt{1+y^2} + \dfrac{1}{\sqrt{1+y^2}} +  \dfrac{y}{\sqrt{1+y^2}} +  \dfrac{\sqrt{1+y^2}}{y} $

となって，両者は一致する。さらにこの関数を$y$で微分して因数分解したものが以下の$h(y)$であり，$h(y)=0$となる$y=1$が極小値を与える。

$h(y) = \dfrac{y-1}{y^2(1+y^2)^{3/2}} \Bigl\{(1+y+y^2+y^3)\bigl(\,1+\sqrt{1+y^2}\,\bigr)+y^4 \Bigr\}$

つまり，関数の極小値を与える条件とその値は，$f(x)$では，

$\tan x = 1 \quad \therefore x = \pi /4 = 0.785398,\quad  f(x) = 2 + 3 \sqrt{2} $

であり，$fh(x)$では，

$\sinh x = 1 \quad \therefore x = \log(\sqrt{2} + 1) = 0.881374, \quad fh(x) = 2+3 \sqrt{2}$

となる。というわけで与えられた三角関数と双曲線関数の極小値は一致した。

三角関数と双曲線関数の間には次の対応があるというのが鍵だった。
\begin{equation}
\begin{aligned}
\sinh x  & \longleftrightarrow \tan x \\
\dfrac{1}{\cosh x} & \longleftrightarrow \cos x \\
\tanh x & \longleftrightarrow \sin x
\end{aligned}
\end{equation}
- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
In[1]:= f[x_] := Sin[x] + Cos[x] + Tan[x] + Csc[x] + Sec[x] + Cot[x]
In[2]:= g[x_] = D[f[x], x]
Out[2]= Cos[x] - Cot[x] Csc[x] - Csc[x]^2 + Sec[x]^2 - Sin[x] + 
 Sec[x] Tan[x]

In[3]:= Factor[c - c/s^3 - 1/s^2 + 1/c^2 - s + s/c^3]
Out[3]= ((c - s) (-c^3 - 2 c^2 s - 2 c s^2 - s^3 + c^3 s^3))/(c^3 s^3)

In[4]:= a = x /. Solve[Cos[x] == Sin[x] && x > 0 && x < 1, x, Reals][[1]]
Out[4]= -2 ArcTan[1 - Sqrt[2]]
In[5]:= fa = f[a] // FullSimplify
Out[5]= 2 + 3 Sqrt[2]

In[6]:= fh[x_] := 
 Sinh[x] + Cosh[x] + Tanh[x] + Csch[x] + Sech[x] + Coth[x]
In[7]:= gh[x_] = D[fh[x], x]
Out[7]= Cosh[x] - Coth[x] Csch[x] - Csch[x]^2 + Sech[x]^2 + Sinh[x] - Sech[x] Tanh[x]

In[8]:= cc = Sqrt[1 + ss^2]
Out[8]= Sqrt[1 + ss^2]
In[9]:= Factor[cc - cc/ss^2 - 1/ss^2 + 1/cc^2 + ss - ss/cc^2]
Out[9]= (1/(ss^2 (1 + ss^2)))(-1 + ss) (1 + ss + ss^2 + ss^3 + ss^4 + Sqrt[1 + ss^2] + ss Sqrt[1 + ss^2] + ss^2 Sqrt[1 + ss^2] + ss^3 Sqrt[1 + ss^2])

In[10]:= b = x /. Solve[Sinh[x] == 1 && 0 < x && x < 1, x, Reals][[1]]
Out[10]= ArcSinh[1]
In[11]:= fb = fh[b] // Simplify
Out[11]= 2 + 3 Sqrt[2]

In[12]:= N[{a, b, f[a], fh[b]}]
Out[12]= {0.785398, 0.881374, 6.24264, 6.24264}
In[13]:= Plot[{f[x], g[x], fh[x], gh[x]}, {x, 0, Pi/2}]
- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -

図　三角関数f(x) 双曲線関数fh(x)とそれらの微分 g(x) gh(x) のグラフ

ab+bc+cd=n

Mathtodonに@antimonさんがこんな問題を出していた。

【問題1】S(n) を「 ab+bc+cd=n (a,b,c,d≥1) の整数解の個数」とする（例： S(5)=5 ）。 S(k)=S(k+1) となる最小の整数 k(≥3)を求めよ。

【問題2】kを 問題1 の解とする時、S(S(S(S(S(k))))) を求めよ。

で，@栄造さんにならって，juliaで解いてみた。
- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
function s(n)
  m=0
  for b in 1:ceil(Int,(n-1)/2)
    for c in 1:ceil(Int,min((n-1)/2,n/b))
      for a in 1:ceil(Int,(n-c)/b-c)
        for d in 1 :ceil(Int,(n-a*b)/c-b)
          if n == a*b + b*c + c*d
#           println(a," ",b," ",c," ",d)
            m = m+1
          end
        end
      end
    end
  end
  return m
end

for k in 3:20
  println(k,":",s(k))
end

@time println(s(14))
@time println(s(s(14)))
@time println(s(s(s(14))))
@time println(s(s(s(s(14)))))
@time println(s(s(s(s(s(14))))))
- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
3:1
4:2
5:5
6:6
7:11
8:13
9:17
10:22
11:27
12:29
13:37
14:44
15:44
16:55
17:59
18:68
19:71
20:81
44
  0.000135 seconds (38 allocations: 1.047 KiB)
319
  0.000084 seconds (36 allocations: 1.156 KiB)
4256
  0.001191 seconds (37 allocations: 880 bytes)
178474
  0.270975 seconds (187 allocations: 11.359 KiB)
13153386
788.437834 seconds (186 allocations: 10.188 KiB)

juliaをたまに使うと，割り算の整数化やかけ算記号が省略できないことなどでつまずく。工夫のないプログラムなので時間はやたらにかかってしまう。

数値計算のリスク

精度保証付き数値計算についてのQiitaのAdvent Calendarの記事が話題になっていた。数値計算はなかなか奥が深いので困る。

[Rumpの例題]
$f(a,b) = 333.75 b^6 + a^2 (11 a^2 b^2 − b^6−121 b^4−2) + 5.5 b^8 +\dfrac{a}{2b}$
に $(a,b)=(77617.0, 33096.0)$ を代入した値は？

Mathematicaの場合

In[1]:= f[a_, b_] :=  333.75 b^6 + a^2 (11 a^2 b^2 - b^6 - 121 b^4 - 2) + 5.5 b^8 + a/(2 b)
In[2]:= f[77617.0, 33096.0]
Out[2]= -1.18059*10^21

In[3]:= g[a_, b_] :=  1335/4 b^6 + a^2 (11 a^2 b^2 - b^6 - 121 b^4 - 2) + 11/2 b^8 + a/(2 b)
In[4]:= N[g[77617, 33096], 20]
Out[4]= -0.82739605994682136814

Juliaの場合

[1] function g(a::BigInt,b::BigInt)
    x = 1335/4*b^6 + a^2*(11*a^2*b^2 - b^6 - 121*b^4 - 2) + 11/2*b^8 + a/(2*b)
end
[2] g(BigInt(77617), BigInt(33096))
[2] -0.8273960599468213681411650954798162919990331157843848199178148416727096930142628

[3] function g128(a::Int128,b::Int128)
   x = 1335/4*b^6 + a^2*(11*a^2*b^2 - b^6 - 121*b^4 - 2) + 11/2*b^8 + a/(2*b)
end
[4] g128(Int128(77617), Int128(33096))
[4] 1.1805916207174113e21

[5] function f(a::BigFloat,b::BigFloat)
    x = 1335/4*b^6 + a^2*(11*a^2*b^2 - b^6 - 121*b^4 - 2) + 11/2*b^8 + a/(2*b)
end
[6] f(BigFloat(77617), BigFloat(33096))
[6] -0.8273960599468213681411650954798162919990331157843848199178148416727096930142628

[7] function f64(a::Float64,b::Float64)
    x = 1335/4*b^6 + a^2*(11*a^2*b^2 - b^6 - 121*b^4 - 2) + 11/2*b^8 + a/(2*b)
end
[8] f(Float64(77617), Float64(33096))
[8] -1.1805916207174113e21

円周率プール

円周率の求め方には様々あっておもしろい。最近再び話題になっていたのが，2003年にGalperinが出した論文，"Playing Pool with Pi (The Numer π from a Billiard Point of View)" とその動画。プールはビリヤード台のことかと思っていたら，ポケットビリヤードのことだった。穴に落ちたビリヤードボールがたまるのでプールらしい。

質量の異なる２球と壁の弾性衝突から円周率がみごとに求まる理論の詳しい説明は，京都府立嵯峨野高等学校の橋本雄馬先生の「物体の衝突と円周率」にある。とてもわかりやすく丁寧な説明がされている。

動画の方もいろいろあるようだが，"The Most Unexpected Answer to A Counting Puzzle"がよかった。

この衝突計算機で他の定数が出ないかを考えようとしたけれど，なかなか難しそうだったので３分で挫折した。

蛙飛び法

ファインマン物理学の第Ｉ巻の第９章に蛙跳び法による運動のシミュレーションが取り上げられている。バネの運動の場合，運動方程式は，$m \ddot{x} = -k x$であるが，これを$\dot{x}=v$と$\dot{v}= -k/m x = -\lambda x$としてオイラー法を適用する。$\epsilon=t_{n+1}-t_n, \ f_n=f(t_n)$などとして，
前進差分は，
\begin{equation}
\begin{aligned}
x_{n+1}=x_{n}+\epsilon v_{n}\\
v_{n+1}=v_{n}- \lambda \epsilon x_{n}
\end{aligned}
\end{equation}
後退差分は，
\begin{equation}
\begin{aligned}
x_{n+1}=x_{n}+\epsilon v_{n+1}\\
v_{n+1}=v_{n}- \lambda \epsilon x_{n+1}
\end{aligned}
\end{equation}
中心差分は，
\begin{equation}
\begin{aligned}
x_{n+1}=x_{n-1}+2\epsilon v_{n}\\
v_{n+1}=v_{n-1}- 2\lambda \epsilon x_{n}
\end{aligned}
\end{equation}
中心差分の片方をずらすと蛙跳び法の表式が得られる。
\begin{equation}
\begin{aligned}
x_{n+2}=x_{n}+2\epsilon v_{n+1}\\
v_{n+1}=v_{n-1}- 2\lambda \epsilon x_{n}
\end{aligned}
\end{equation}
一方，前進差分と後退差分は，次のように表せる。
\begin{equation}
\begin{aligned}
\begin{pmatrix}x_{n+1} \\ v_{n+1}\end{pmatrix} &=
\begin{pmatrix} 1 & \epsilon \\ - \lambda \epsilon & 1 \end{pmatrix}
\begin{pmatrix}x_{n} \\ v_{n}\end{pmatrix} \\
\begin{pmatrix} 1 & -\epsilon \\ \lambda \epsilon & 1 \end{pmatrix}
\begin{pmatrix}x_{n+1} \\ v_{n+1}\end{pmatrix}
&= \begin{pmatrix}x_{n} \\ v_{n}\end{pmatrix}
\end{aligned}
\end{equation}
陰解法となっている後退差分を解いて$ o(\epsilon^2)$まで考えると，
\begin{equation}
\begin{pmatrix}x_{n+1} \\ v_{n+1}\end{pmatrix}
=\begin{pmatrix}\dfrac{1}{1+\lambda \epsilon^2} & \epsilon \\
-\lambda \epsilon &  \dfrac{1}{1+\lambda \epsilon^2}\end{pmatrix}
\begin{pmatrix}x_{n} \\ v_{n}\end{pmatrix}
\end{equation}
前進差分と後退差分の平均をとると，中心差分に相当するものが得られる。
\begin{equation}
\begin{pmatrix}x_{n+1} \\ v_{n+1}\end{pmatrix}
=\begin{pmatrix}1 - \lambda \epsilon^2 /2 & \epsilon \\
-\lambda \epsilon &  1 -\lambda \epsilon^2 /2 \end{pmatrix}
\begin{pmatrix}x_{n} \\ v_{n}\end{pmatrix}
\end{equation}

山羊問題

山羊問題（Goat Problem）は次のような問題である。中心Ａ，半径$r=1$の草の生えた円形の土地Ｓがある。その周の１点Ｏから長さ$a$のヒモにつながれた山羊を放し飼いにすると，Ｓのうち，半径$a$のOを中心とし半径$a$の円内の草が食べられてしまう。その面積がＳの半分になるようなヒモの長さ$a$はいくらか？図形はOAを結ぶ線に対称なので，半分だけ考えてみよう。

図　山羊問題

山羊が食べた草地の面積は，扇型O-BP+扇型A-OP-三角形AOPであり，これが$\pi r^2/4$になればよい。角POA=$\phi$とすると，角PAO=$\pi-2\phi$である。これを式で表すと，

\begin{equation}
\begin{aligned}
\dfrac{\pi r^2}{4} &= \dfrac{r^2}{2}(\pi - 2 \phi) + \dfrac{a^2}{2} \phi - \dfrac{r^2}{2} \sin 2 \phi \\
a &= 2 r \cos \phi
\end{aligned}
\end{equation}
したがって，
\begin{equation}
4 \phi \cos^2 \phi = \sin 2 \phi +2 \phi -\dfrac{\pi}{2}
\end{equation}
これをMathematicaで解くと，$a/r = 1.15873$となった。
- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
In[1]:= Clear[x]; sol1 = FindRoot[4 Cos[x]^2  x == Sin[2 x] + 2 x - Pi/2, {x, 1}]; x = x /. sol1
Out[1]= 0.952848
In[2]:= a = 2 Cos[x]
Out[2]= 1.15873
In[3]:= Clear[x]; sol2 = FindRoot[Sqrt[1 - (x - 1)^2] == Sqrt[a^2 - x^2], {x, 1}]; b = x /. sol2
Out[3]= 0.671326
In[4]:= c = NIntegrate[Sqrt[1 - (x - 1)^2], {x, 0, b}] + NIntegrate[Sqrt[a^2 - x^2], {x, b, a}]
Out[4]= 0.785398

In[5]:= g1 = Plot[{Sqrt[a^2 - x^2], Sqrt[1 - (x - 1)^2],
   Sqrt[a^2 - b^2]/b x, -Sqrt[a^2 - b^2]/(a - b) (x - a), -Sqrt[a^2 - b^2]/(1 - b) (x - 1)}, {x, 0, 2},
  AspectRatio -> Automatic, PlotStyle -> {, , Dashed, Dashed, Dotted}, PlotRange -> {0, 1.2}]
In[6]:= g2 = Graphics[{Text[O, {0.05, 0.03}], Text[A, {0.95, 0.03}],
   Text[B, {1.20, 0.03}], Text[P, {0.69, 1.0}]}];
- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -