芥川龍之介が「蜘蛛の糸」を発表して百年。高二の秋の文化祭,クラスの仮装行列のテーマが 蜘蛛の糸だった。お釈迦様の極楽タワーの竹を近所から切り出し,地獄の焔と煙の絵を描いた。犍陀多に続いて蜘蛛の糸(登山部の赤いザイル)に群がる地獄の亡者だったころ。
2023年10月20日金曜日
円筒座標のベクトル解析
2023年10月19日木曜日
処理水と廃炉
2023年10月18日水曜日
恒星間天体
2023年10月17日火曜日
久々のJulia
function dt(N,eps)# N=1000000# eps = 1.0e-6ratio = log(2)/log(3)for i in 1:Njmin = floor(Int64,i*ratio)jmax = ceil(Int64,i*ratio)for j in jmin:jmaxsol = i*log(2) - j*log(3)if abs(sol) < epsprintln(" 2**",i,"/","3**",j," = ",exp(sol))endendendendfor k = 1:8N=10^keps=1/Nprintln("N=",N," eps=",eps)@time(dt(N,eps))end
N=10 eps=0.12**8/3**5 = 1.05349794238683050.000176 seconds (98 allocations: 2.750 KiB)N=100 eps=0.012**84/3**53 = 0.99791404625730830.000160 seconds (97 allocations: 2.562 KiB)N=1000 eps=0.0010.000003 secondsN=10000 eps=0.00012**1054/3**665 = 0.99995634684218582**2108/3**1330 = 0.99991269558996990.000351 seconds (207 allocations: 5.609 KiB)N=100000 eps=1.0e-52**50508/3**31867 = 0.99999273508457530.000408 seconds (103 allocations: 2.656 KiB)N=1000000 eps=1.0e-62**301994/3**190537 = 1.00000006449409032**603988/3**381074 = 1.00000012898818482**905982/3**571611 = 1.00000019348228350.003297 seconds (311 allocations: 8.562 KiB)N=10000000 eps=1.0e-72**301994/3**190537 = 1.00000006449409030.027930 seconds (105 allocations: 4.938 KiB)N=100000000 eps=1.0e-82**85137581/3**53715833 = 0.99999999254941940.264204 seconds (229 allocations: 17.953 KiB)
いちおうできたことにしておこう。
2023年10月16日月曜日
導体球(4)
2023年10月15日日曜日
導体球(3)
2023年10月14日土曜日
物理学科同窓会(2)
2023年10月13日金曜日
PBL
Q:「課題の設定者が教員か生徒か」「課題が教科限定的か学際的か」「評価のポイントはプロセスかアウトプットか」「期間は短いか長いか」という観点では,問題解決型学習(Problem Based Learning)と課題探究型学習(Project based Learning)の違いがどうなりますか。
A:以下は、問題解決型学習(PBL)と課題探究型学習(PjBL)の違いをそれぞれの観点で比較したものです。課題の設定者が教員か生徒か:PBL: 問題の設定者は通常教員であり、学習者に対して特定の問題を提供します。PjBL: 学習者が自ら興味や関心に基づいてプロジェクトを選び、課題を設定します。課題が教科限定的か学際的か:PBL: 問題は通常特定の教科に関連しており、その教科における問題解決を中心に学習が行われます。PjBL: 課題は学際的であり、複数の教科を組み合わせてプロジェクトを通じて学習が行われます。評価のポイントはプロセスかアウトプットか:PBL: 評価の重点は、問題解決のプロセス、つまり学習者がどれだけ効果的に問題に取り組んだかに置かれます。PjBL: 評価はプロジェクトのアウトプット、つまり成果物やプロジェクトの完成度に焦点を当てます。期間は短いか長いか:PBL: 問題解決の期間は比較的短い場合が多く、特定の問題に対処する短期的な活動が一般的です。PjBL: プロジェクトの期間は通常長く、複数の週や学期にわたって続く場合があります。これらの要素に基づいて、PBLとPjBLは異なるアプローチを取ります。PBLは特定の問題に焦点を当て、その解決策を見つけるためのプロセスに重点を置きます。一方、PjBLは学習者の興味や関心を反映したプロジェクトを通じて、幅広い学際的な学びを促進します。
これはあくまでもChatGPTの見解 (もしかすると平均的な世論)であることに注意が必要。これにアクティブラーニングの定義をどうするか問題を加えるとさらに混乱は必至である。
[1]今、求められる力を高める総合的な探究の時間の展開(小学校編,文部科学省)
2023年10月12日木曜日
導体球(2)
2023年10月11日水曜日
導体球(1)
2023年10月10日火曜日
2023年10月9日月曜日
2023年10月8日日曜日
2023年10月7日土曜日
2023年10月6日金曜日
2023年10月5日木曜日
2023年10月4日水曜日
2023年10月3日火曜日
2023年10月2日月曜日
2023年10月1日日曜日
中秋の名月
2023年9月30日土曜日
万博会場
Q:2025年の国際博覧会の大阪府内の候補地が夢洲を含めて7箇所あったそうですが,それはどこですか。A:2025年の国際博覧会の大阪府内の候補地は、以下の7箇所です。・彩都東部+万博記念公園(茨木市・大阪市)・服部緑地(豊中市)・花博記念公園鶴見緑地(大阪市)・舞洲(大阪市此花区)・大泉緑地(堺市)・りんくう公園+りんくうタウン(泉佐野市・大阪市)・夢洲(大阪市此花区)2015年7月28日の検討会第4回会合では、上記7箇所が例示されました。その後、2016年5月の報道によると、候補地に夢洲も追加されました。最終的に、2025年の国際博覧会の開催地は、夢洲に決定しました。
2023年9月29日金曜日
再処理工場
2023年9月28日木曜日
理系五割
例えば、現行の数理・データサイエンス・AI の習得目標に加えて、理工系分野の学問を専攻する女子学生の割合を7%から男子学生と同等の 28%程度に高めていくことや、成長分野への転換と併せて学生が複数専攻などにより文理の枠を超えた学修に取り組むことができる環境を整えることを前提とした上で、現在 35%にとどまっている自然科学(理系)分野の学問を専攻 する学生の割合について OECD 諸国で最も高い水準である5割程度を目指すなど、まあ,そういうことです。OECD諸国は4割前後,最高が英国の45%,フランスは31%なので,全然無理する必要はないはずが,これでさらに混乱が加速しそうな雰囲気がただよう。教育未来創造会議第一次提言のポイントはわかりやすく整理されているが,全12ページのうち7ページが委員の人物紹介になっている。
2023年9月27日水曜日
トリチウム(2)
2023年9月26日火曜日
iPhone15
iPhone15 iPhoneSE2023 Sep 2020 Apr139,800円 69,800円A16 Bionic A13 Bionic3.5GHz 2.66GHz6コアCPU 6コアCPU5コアGPU 4コアGPU16コアNE 8コアNE256GB 128GB6.1インチOLED 4.7インチLCD2556×1179ピクセル 1334×759ピクセル460dpi 326dpi2,000,000:1 1,400:11000ニト 625ニト48MPメイン|超広角 12MPシングル12MPフロント 7MPフロントズーム .5× 1× 2× ズーム 1×USB-C/USB2 Lightning/USB2FaceID TouchID5G 4G/LTEBlueTooth5.3 BlueTooth5.0MagSafe —20時間ビデオ 13時間ビデオ80時間オーディオ 40時間オーディオ147.6×71.6×7.8 138.4×67.3×7.3171g 148g
少なくとも,この近所に5Gの電波が届くまではいらないかな。
2023年9月25日月曜日
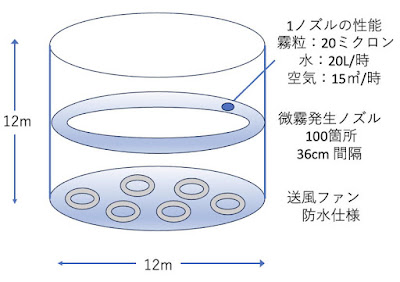
水蒸気放出(3)
2023年9月24日日曜日
水蒸気放出(2)
2023年9月23日土曜日
水蒸気放出(1)
| 気温 | 湿度 * | 風速 | 晴日 ≧40% | 蒸発量 | 蒸発量+ | |
| 1月 | 2.2 | 58 | 2.0 | 22.5 | 0.15 | 0.30 |
| 2月 | 2.7 | 59 | 2.0 | 20.6 | 0.16 | 0.31 |
| 3月 | 5.7 | 62 | 2.2 | 19.5 | 0.19 | 0.38 |
| 4月 | 10.7 | 68 | 2.1 | 17.9 | 0.22 | 0.43 |
| 5月 | 15.5 | 76 | 1.8 | 16.5 | 0.22 | 0.51 |
| 6月 | 18.8 | 83 | 1.5 | 11.7 | 0.17 | 0.50 |
| 7月 | 22.6 | 86 | 1.3 | 11.4 | 0.17 | 0.53 |
| 8月 | 24.0 | 84 | 1.4 | 14.9 | 0.22 | 0.62 |
| 9月 | 20.6 | 80 | 1.4 | 12.2 | 0.22 | 0.56 |
| 10月 | 15.1 | 75 | 1.4 | 14.9 | 0.19 | 0.45 |
| 11月 | 9.7 | 69 | 1.6 | 19.1 | 0.17 | 0.38 |
| 12月 | 4.7 | 62 | 1.8 | 21.0 | 0.17 | 0.32 |
| 全体 | 12.7 | 72 | 1.7 | 201.9 | 0.19 | 0.45 |
2023年9月22日金曜日
フィンランドの教育(2)
2023年9月21日木曜日
フィンランドの教育(1)
フィンランドの教育・文化省が, 現状をレビューした報告を2023年1月に出していて,その英文要約を見ることができる。これをChatGPTで更に要約して,DeepLで翻訳したものを次に示す。
フィンランドの教育・文化省は、フィンランドの教育・文化セクターの過去数十年の変遷に焦点を当てた初の「ビルドゥング・レビュー」を発表した。主なポイントは以下の通り:
歴史的概観: 1950年代から1990年代初頭にかけて、フィンランドの教育部門は大きな成長を遂げた。総合学校、高等教育の改革、高等教育の拡大により、より多くのフィンランド人が教育を受けられるようになった。1990年代初頭には、図書館や芸術機関のネットワークも充実した。
1990年代の課題: 1990年代には教育資金が削減され、若者の教育レベルの上昇が止まり、学習成果が低下した。図書館もまた、様々な芸術分野への助成が減少し、利用者の減少という課題に直面した。
最近の動き: 2010年代半ば以降、就学前義務教育が導入され、義務教育が延長された。特にコロナウイルス危機の際には、高等教育の機会も拡大した。2030年までに研究開発資金を増強する必要性についてはコンセンサスが得られている。
学習成果: フィンランドでは2000年代前半、特に読解力と数学の学習成果が急速に低下した。しかし、国際比較では、フィンランドの学生の成績は依然として良好である。社会的背景や性別による学習成果の格差が拡大している。
教育レベル: フィンランド国民の教育レベルは低下しており、1978年生まれは最も教育水準が高い。しかし、最近の傾向では、より若い年齢層がこのレベルを上回る可能性がある。
教職: フィンランドの教職は年々尊敬を集めており、フィンランドの教育制度の学術的教育と国際的評価が重要な役割を果たしている。
研究開発: 研究者の数は、特に企業部門で急増している。大学も研究範囲を広げている。
公共図書館: 1990年代には公共図書館への資金援助が減少し、図書購入の減少や貸出者数の減少につながった。
文化・芸術: 文化分野は、雇用の減少など困難に直面している。しかし、映画など様々な芸術の観客は増加している。
スポーツ: 成人のスポーツ参加率は依然として高いが、学童の有酸素運動能力は低下している。自治体によるスポーツ施設の建設は、年々変動している。
学資援助: 学生支援:1990年代の不況以降、学生支援にかかる費用は減少している。
これが,いまさらながらネットで取り上げられて(フィンランド教育は失敗だったとフィンランド政府が公式に認めました), フィンランド教育をディスる輪が広がっている。まあ,こういう自己分析ができるだけよいと思う。日本の文部科学省や政府は自分の政策が間違っていたとは絶対に認めないだろう。
[1]OECD生徒の学習到達度調査(PISA)(国立教育政策研究所)
2023年9月20日水曜日
古稀
唐の詩人杜甫の詩・曲江(きょっこう)「酒債(しゅさい)は尋常行く処(ところ)に有り 人生七十古来稀なり」(酒代の付けは私が普通行く所には、どこにでもある(しかし)七十年生きる人は古くから稀である)が典拠。
朝 回 日 日 典 春 衣毎 日 江 頭 尽 酔 帰酒 債 尋 常 行 処 有人 生 七 十 古 来 稀穿 花 蛱 蝶 深 深 見点 水 蜻 蜓 款 款 飛伝 語 風 光 共 流 転暫 時 相 賞 莫 相 違
春の衣を質入するのだからどの季節かと思えば,花に蝶が飛ぶ春だった。この詩の時代は盛唐(710-766),日本の奈良時代である。曲江は長安の東南隅に作られた池で現在は一面の畑というのは昔の話。
還暦は満60歳数えで61歳の祝いだが,古稀は満69歳,数えで70歳に対応する。で,本日9月20日(空の日)で満70歳の自分にとっては古稀が終る日になる。しばらく前から気分はずっと70歳だったのでそれはそれでよし。
2023年9月19日火曜日
テクタイト
2023年9月18日月曜日
開放型イヤフォン
JVC Kenwood nearphone 11,77516mmドライバ,本体7時間+ケース10時間,BT5.1ambie sound earcuffs 15,339?ドライバ,本体6時間+ケース12時間,BT5.2OneOdeo OpenRock Pro 16,89016.2mmドライバ,本体19時間+ケース46時間,BT5.2SONY RingBuds 18,71712mmドライバ,本体5.5時間+ケース12時間,BT5.2,マルチポイントOladance Wearable Stereo 20,98016.5mmドライバ,本体10時間 | 16時間,BT5.2Cleer ARC 22,80016.2mmドライバ,本体7時間+ケース11時間,BT5.0
Shokz OpenFit 24,880?mmドライバ,本体7時間+ケース28時間,BT5.2
Oladance OWS Pro 34,80023*10mmドライバ,本体16時間+ケース42時間,BT5.3,マルチポイント