　　　　On a Thread of the Web: 基本再生産数と集団免疫率

2020年3月27日金曜日

基本再生産数と集団免疫率

感染症数理の基本的なモデルであるSIRモデルについて自分は十分理解できていなかった。奈良女子大の高須さん[1]や神戸大の牧野さん[2]や京大の門さん[3]の資料が大変わかりやすくて勉強になった。

きっかけはツイッター@nagayaさんの次のコメント。

R0＝2なら国民の50%、3なら66%、逆に1.5なら33%の免疫獲得で理論上は収束に向かいます（この理論値を超えて免疫獲得した分が「オーバーシュート」）。日本は自粛とクラスター追跡、検査を絞って1.2程度にして医療崩壊を避けようとしたんでしょう。無理です。長期化しますし、指数関数的に潜在します。

基本再生産数$R_0$と集団免疫率に関係あったっけ？ということで高須さんの資料で学び直し。

SIRモデルは，感受性保持者（Susceptible，$S(t)$）・感染者（Infected，$I(t)$）・免疫保持者（Recovered，$R(t)$ ）からなる力学系モデルであり次の微分方程式を満たす（$\beta, \gamma$の定義に注意）。ここで$t$は時間であり，最も単純なバージョンでは集団の人数を$N$として$S(t)+I(t)+R(t)=N$は保存量である。なお，$\beta$は感染率（１人単位時間当りの感染数），$\gamma$は感染期間である。
\begin{equation}
\begin{aligned}
\dfrac{dS}{dt} &= -\beta \dfrac{S}{N} I\\
\dfrac{dI}{dt} &= \beta \dfrac{S}{N} I - \dfrac{I}{\gamma} \\
\dfrac{dR}{dt} &= - \dfrac{I}{\gamma}\\
\end{aligned}
\end{equation}
これからわかること。集団中の感受性保持者（免疫非保持者）の割合を$p(t)=\dfrac{S}{N} $とすると，$p(t) > \dfrac{1}{\beta \gamma}$で感染拡大，$p(t) < \dfrac{1}{\beta \gamma}$で感染縮小となる。そこで，基本再生産数を$R_0 = \beta \gamma$と定義すると，$p(0)=1$の初期状態において，$R_0>1$で感染拡大，$R_0<1$で感染縮小となる。なお，実効再生産数が$R_{\rm eff}=R_0 p(t)$ と定義される。

また集団免疫率を$\pi(t) = 1-p(t)$と定義すると，感染拡大と縮小の分岐点$\tau$では，$1-\pi(\tau) = \dfrac{1}{R_0}$である。これが@nagayaさんの示した関係式だった。

次に十分時間がたって$I(\infty)=0$となるときの集団免疫率$\pi(\infty)$と$R_0$の関係を求めてみよう。もとの微分方程式系の第１式と第３式から次の微分方程式が得られる。
\begin{equation}
\begin{aligned}
\dfrac{dS}{dR} &= -R_0 \dfrac{S}{N}\\
\dfrac{dS}{S} &= -R_0 \dfrac{dR}{N}\\
\log S + C &= -R_0 \dfrac{R}{N} = -R_0 (1-\dfrac{I}{N} - p(t) ) = -R_0 (\pi(t) - i(t) )\\
\end{aligned}
\end{equation}
ただし，$i(t)=\dfrac{I}{N}$であり，$i(\infty)=0$。そこで，$S(0)=N$として$\pi(\infty)=\pi$とすると，
\begin{equation}
\begin{aligned}
\dfrac{S(t)}{S(0)} &= e^{-R_0\{ \pi(t) - i (t) \}} \\
p(t) = 1-\pi(t) &= e^{-R_0\{ \pi(t) - i (t) \}} \\
1- \pi &= e^{ -R_0 \pi } \\
R_0 &= - \dfrac{1}{\pi}\log (1- \pi )
\end{aligned}
\end{equation}

図１　t=∞における集団免疫率π（横軸）と基本再生産数R0（縦軸）

分岐点における$\pi(t)$と$R_0$の関係式とは異なった関係を与えていることに注意しよう。

付録：juliaにおける上記プロットのコード
- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
using Plots
gr()
x = 0.05:0.05:0.95
f(x) = .- 1 ./ x .* log.(1 .- x)
y = f(x)
plot(x, y, label="")
savefig("sir.png")
- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -

追伸：
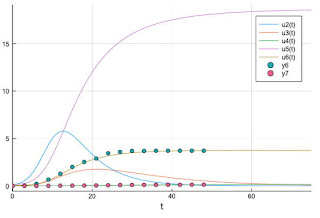
以上は簡単なSIRモデルの場合だが，湖北省（武漢以外）をおおむね説明したSIIDR2モデルにたいして，十分な時間がたったときの湖北省（武漢以外）の集団免疫率はどのように推定できるだろうか。パラメタセット，$\alpha_1=5/0.80, \alpha_2=5/0.20, \gamma_1=15/0.96, \gamma_2=15/0.04, \beta=0.915, \nu=0.025, \lambda=7, \tau=7$について計算すると，Recovered $u_5$は1万人当り19程度に収束し，集団免疫率はたかだか0.2%にどどまる。