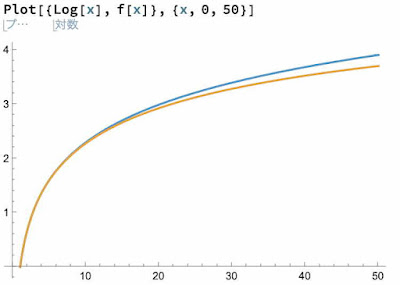
図:Mathematicaで Log[x]とf[x_] := 6 (x - 1)/(x + 1 + 4 Sqrt[x]) を計算
その説明でパデ近似と関係があるようなニュアンスを見かけた。パデ近似はよく耳にしているけれどちゃんと勉強したことはない(あるいはきれいに忘れてしまったか)。
そこで,ちょっと調べてみた。
ある関数 $f(x) = c_0 + c_1 x + c_2 x^2 + \cdots + c_{m+n}x^{m+n}+ \cdots , c_k=\dfrac{f^{(k)}(0)}{k!}$ を 有理多項式$P_{m,n}(x) = \dfrac{a_0+a_1 x + a_2 x^2 + \cdots + a_m x^m}{1 + b_1 x + b_2 x^2 + \cdots + b_n x^n}$で近似するのがパデ近似だ。
$P_{m,n}(x)^{(k)}(0) = f^{(k)}(0), \quad (k=1,\cdots, m+n)$が成り立つように $P_{m,n}$ を定める。つまり,$f(x)$と$P_{m,n}(x) $が,$x=0$におけるテイラー展開の$m+n$次まで一致するということだ。係数全体を定数倍してもパデ近似は不変なので,$b_0=1$とする。
つまり,$c_k, \ \ (k=0,\cdots , m+n)$が与えられているときに,$a_i, \ (i=0, \cdots m)$ $b_j, \ (j=1, \cdots n) $ を求めるという問題だ。そこで,
$\dfrac{a_0+a_1 x + a_2 x^2 + \cdots + a_m x^m}{1 + b_1 x + b_2 x^2 + \cdots + b_n x^n} - (c_0 + c_1 x + c_2 x^2 + \cdots + c_{m+n}x^{m+n} ) = $
($x$の$m+n+1$次以上の多項式X)
$a_0+a_1 x + a_2 x^2 + \cdots + a_m x^m =$
$ (1 + b_1 x + b_2 x^2 + \cdots + b_n x^n )( c_0 + c_1 x + c_2 x^2 + \cdots + c_{m+n}x^{m+n}) -$
($x$の$m+n+1$次以上の多項式Y)
ここで,両辺について$x$の$m+n$次までの係数比較から,
$\displaystyle a_k = \sum_{i=0}^k c_i b_{k-i} \ (k = 0 , \cdots, m+n) $ ,ただし,$ a_j =0 \ (j>m), \ b_j = 0 \ (j > n) $
$a_j=0$となる式が $m+n-m=n$本あって,未知数の$b_j$が$n$個あるので,この連立方程式を解けば,$n$個の$b_j$ がすべて求まる。これを使って,$a_1 \cdots a_m$ が定まる。
0 件のコメント:
コメントを投稿