東京高検検事長の定年延長についての元検察官有志による意見書
1 東京高検検事長黒川弘務氏は、本年2月8日に定年の63歳に達し退官の予定であったが、直前の1月31日、その定年を8月7日まで半年間延長する閣議決定が行われ、同氏は定年を過ぎて今なお現職に止(とど)まっている。
検察庁法によれば、定年は検事総長が65歳、その他の検察官は63歳とされており(同法22条)、定年延長を可能とする規定はない。従って検察官の定年を延長するためには検察庁法を改正するしかない。しかるに内閣は同法改正の手続きを経ずに閣議決定のみで黒川氏の定年延長を決定した。これは内閣が現検事総長稲田伸夫氏の後任として黒川氏を予定しており、そのために稲田氏を遅くとも総長の通例の在職期間である2年が終了する8月初旬までに勇退させてその後任に黒川氏を充てるための措置だというのがもっぱらの観測である。一説によると、本年4月20日に京都で開催される予定であった国連犯罪防止刑事司法会議で開催国を代表して稲田氏が開会の演説を行うことを花道として稲田氏が勇退し黒川氏が引き継ぐという筋書きであったが、新型コロナウイルスの流行を理由に会議が中止されたためにこの筋書きは消えたとも言われている。
いずれにせよ、この閣議決定による黒川氏の定年延長は検察庁法に基づかないものであり、黒川氏の留任には法的根拠はない。この点については、日弁連会長以下全国35を超える弁護士会の会長が反対声明を出したが、内閣はこの閣議決定を撤回せず、黒川氏の定年を超えての留任という異常な状態が現在も続いている。
2 一般の国家公務員については、一定の要件の下に定年延長が認められており(国家公務員法81条の3)、内閣はこれを根拠に黒川氏の定年延長を閣議決定したものであるが、検察庁法は国家公務員に対する通則である国家公務員法に対して特別法の関係にある。従って「特別法は一般法に優先する」との法理に従い、検察庁法に規定がないものについては通則としての国家公務員法が適用されるが、検察庁法に規定があるものについては同法が優先適用される。定年に関しては検察庁法に規定があるので、国家公務員法の定年関係規定は検察官には適用されない。これは従来の政府の見解でもあった。例えば昭和56年(1981年)4月28日、衆議院内閣委員会において所管の人事院事務総局斧任用局長は、「検察官には国家公務員法の定年延長規定は適用されない」旨明言しており、これに反する運用はこれまで1回も行われて来なかった。すなわちこの解釈と運用が定着している。
検察官は起訴不起訴の決定権すなわち公訴権を独占し、併せて捜査権も有する。捜査権の範囲は広く、政財界の不正事犯も当然捜査の対象となる。捜査権をもつ公訴官としてその責任は広く重い。時の政権の圧力によって起訴に値する事件が不起訴とされたり、起訴に値しないような事件が起訴されるような事態が発生するようなことがあれば日本の刑事司法は適正公平という基本理念を失って崩壊することになりかねない。検察官の責務は極めて重大であり、検察官は自ら捜査によって収集した証拠等の資料に基づいて起訴すべき事件か否かを判定する役割を担っている。その意味で検察官は準司法官とも言われ、司法の前衛たる役割を担っていると言える。
こうした検察官の責任の特殊性、重大性から一般の国家公務員を対象とした国家公務員法とは別に検察庁法という特別法を制定し、例えば検察官は検察官適格審査会によらなければその意に反して罷免(ひめん)されない(検察庁法23条)などの身分保障規定を設けている。検察官も一般の国家公務員であるから国家公務員法が適用されるというような皮相的な解釈は成り立たないのである。
3 本年2月13日衆議院本会議で、安倍総理大臣は「検察官にも国家公務員法の適用があると従来の解釈を変更することにした」旨述べた。これは、本来国会の権限である法律改正の手続きを経ずに内閣による解釈だけで法律の解釈運用を変更したという宣言であって、フランスの絶対王制を確立し君臨したルイ14世の言葉として伝えられる「朕(ちん)は国家である」との中世の亡霊のような言葉を彷彿(ほうふつ)とさせるような姿勢であり、近代国家の基本理念である三権分立主義の否定にもつながりかねない危険性を含んでいる。
時代背景は異なるが17世紀の高名な政治思想家ジョン・ロックはその著「統治二論」(加藤節訳、岩波文庫)の中で「法が終わるところ、暴政が始まる」と警告している。心すべき言葉である。
ところで仮に安倍総理の解釈のように国家公務員法による定年延長規定が検察官にも適用されると解釈しても、同法81条の3に規定する「その職員の職務の特殊性またはその職員の職務の遂行上の特別の事情からみてその退職により公務の運営に著しい支障が生ずると認められる十分の理由があるとき」という定年延長の要件に該当しないことは明らかである。
加えて人事院規則11―8第7条には「勤務延長は、職員が定年退職をすべきこととなる場合において、次の各号の1に該当するときに行うことができる」として、①職務が高度の専門的な知識、熟練した技能または豊富な経験を必要とするものであるため後任を容易に得ることができないとき、②勤務環境その他の勤務条件に特殊性があるため、その職員の退職により生ずる欠員を容易に補充することができず、業務の遂行に重大な障害が生ずるとき、③業務の性質上、その職員の退職による担当者の交替が当該業務の継続的遂行に重大な障害を生ずるとき、という場合を定年延長の要件に挙げている。
これは要するに、余人をもって代えがたいということであって、現在であれば新型コロナウイルスの流行を収束させるために必死に調査研究を続けている専門家チームのリーダーで後継者がすぐには見付からないというような場合が想定される。
現在、検察には黒川氏でなければ対応できないというほどの事案が係属しているのかどうか。引き合いに出されるゴーン被告逃亡事件についても黒川氏でなければ、言い換えれば後任の検事長では解決できないという特別な理由があるのであろうか。法律によって厳然と決められている役職定年を延長してまで検事長に留任させるべき法律上の要件に合致する理由は認め難い。
4 4月16日、国家公務員の定年を60歳から65歳に段階的に引き上げる国家公務員法改正案と抱き合わせる形で検察官の定年も63歳から65歳に引き上げる検察庁法改正案が衆議院本会議で審議入りした。野党側が前記閣議決定の撤回を求めたのに対し菅義偉官房長官は必要なしと突っぱねて既に閣議決定した黒川氏の定年延長を維持する方針を示した。こうして同氏の定年延長問題の決着が着かないまま検察庁法改正案の審議が開始されたのである。
この改正案中重要な問題点は、検事長を含む上級検察官の役職定年延長に関する改正についてである。すなわち同改正案には「内閣は(中略)年齢が63年に達した次長検事または検事長について、当該次長検事または検事長の職務の遂行上の特別の事情を勘案して、当該次長検事または検事長を検事に任命することにより公務の運営に著しい支障が生ずると認められる事由として内閣が定める事由があると認めるときは、当該次長検事または検事長が年齢63年に達した日の翌日から起算して1年を超えない範囲内で期限を定め、引き続き当該次長検事または検事長が年齢63年に達した日において占めていた官及び職を占めたまま勤務をさせることができる(後略)」と記載されている。
難解な条文であるが、要するに次長検事および検事長は63歳の職務定年に達しても内閣が必要と認める一定の理由があれば1年以内の範囲で定年延長ができるということである。
注意すべきは、この規定は内閣の裁量で次長検事および検事長の定年延長が可能とする内容であり、前記の閣僚会議によって黒川検事長の定年延長を決定した違法な決議を後追いで容認しようとするものである。これまで政界と検察との両者間には検察官の人事に政治は介入しないという確立した慣例があり、その慣例がきちんと守られてきた。これは「検察を政治の影響から切りはなすための知恵」とされている(元検事総長伊藤栄樹著「だまされる検事」)。検察庁法は、組織の長に事故があるときまたは欠けたときに備えて臨時職務代行の制度(同法13条)を設けており、定年延長によって対応することは毫(ごう)も想定していなかったし、これからも同様であろうと思われる。
今回の法改正は、検察の人事に政治権力が介入することを正当化し、政権の意に沿わない検察の動きを封じ込め、検察の力を殺(そ)ぐことを意図していると考えられる。
5 かつてロッキード世代と呼ばれる世代があったように思われる。ロッキード事件の捜査、公判に関与した検察官や検察事務官ばかりでなく、捜査、公判の推移に一喜一憂しつつ見守っていた多くの関係者、広くは国民大多数であった。
振り返ると、昭和51年(1976年)2月5日、某紙夕刊1面トップに「ロッキード社がワイロ商法 エアバスにからみ48億円 児玉誉士夫氏に21億円 日本政府にも流れる」との記事が掲載され、翌日から新聞もテレビもロッキード関連の報道一色に塗りつぶされて日本列島は興奮の渦に巻き込まれた。
当時特捜部にいた若手検事の間では、この降って湧いたような事件に対して、特捜部として必ず捜査に着手するという積極派や、着手すると言っても贈賄の被疑者は国外在住のロッキード社の幹部が中心だし、証拠もほとんど海外にある、いくら特捜部でも手が届かないのではないかという懐疑派、苦労して捜査しても造船疑獄事件のように指揮権発動でおしまいだという悲観派が入り乱れていた。
事件の第一報が掲載されてから13日後の2月18日検察首脳会議が開かれ、席上、東京高検検事長の神谷尚男氏が「いまこの事件の疑惑解明に着手しなければ検察は今後20年間国民の信頼を失う」と発言したことが報道されるやロッキード世代は歓喜した。後日談だが事件終了後しばらくして若手検事何名かで神谷氏のご自宅にお邪魔したときにこの発言をされた時の神谷氏の心境を聞いた。「(八方塞がりの中で)進むも地獄、退くも地獄なら、進むしかないではないか」という答えであった。
この神谷検事長の国民信頼発言でロッキード事件の方針が決定し、あとは田中角栄氏ら政財界の大物逮捕に至るご存じの展開となった。時の検事総長は布施健氏、法務大臣は稲葉修氏、法務事務次官は塩野宜慶(やすよし)(後に最高裁判事)、内閣総理大臣は三木武夫氏であった。
特捜部が造船疑獄事件の時のように指揮権発動に怯(おび)えることなくのびのびと事件の解明に全力を傾注できたのは検察上層部の不退転の姿勢、それに国民の熱い支持と、捜査への政治的介入に抑制的な政治家たちの存在であった。
国会で捜査の進展状況や疑惑を持たれている政治家の名前を明らかにせよと迫る国会議員に対して捜査の秘密を楯(たて)に断固拒否し続けた安原美穂刑事局長の姿が思い出される。
しかし検察の歴史には、捜査幹部が押収資料を改ざんするという天を仰ぎたくなるような恥ずべき事件もあった。後輩たちがこの事件がトラウマとなって弱体化し、きちんと育っていないのではないかという思いもある。それが今回のように政治権力につけ込まれる隙を与えてしまったのではないかとの懸念もある。検察は強い権力を持つ組織としてあくまで謙虚でなくてはならない。
しかしながら、検察が萎縮して人事権まで政権側に握られ、起訴・不起訴の決定など公訴権の行使にまで掣肘(せいちゅう)を受けるようになったら検察は国民の信託に応えられない。
正しいことが正しく行われる国家社会でなくてはならない。
黒川検事長の定年延長閣議決定、今回の検察庁法改正案提出と続く一連の動きは、検察の組織を弱体化して時の政権の意のままに動く組織に改変させようとする動きであり、ロッキード世代として看過し得ないものである。関係者がこの検察庁法改正の問題を賢察され、内閣が潔くこの改正法案中、検察幹部の定年延長を認める規定は撤回することを期待し、あくまで維持するというのであれば、与党野党の境界を超えて多くの国会議員と法曹人、そして心ある国民すべてがこの検察庁法改正案に断固反対の声を上げてこれを阻止する行動に出ることを期待してやまない。
【追記】この意見書は、本来は広く心ある元検察官多数に呼びかけて協議を重ねてまとめ上げるべきところ、既に問題の検察庁法一部改正法案が国会に提出され審議が開始されるという差し迫った状況下にあり、意見のとりまとめに当たる私(清水勇男)は既に85歳の高齢に加えて疾病により身体の自由を大きく失っている事情にあることから思うに任せず、やむなくごく少数の親しい先輩知友のみに呼びかけて起案したものであり、更に広く呼びかければ賛同者も多く参集し連名者も多岐に上るものと確実に予想されるので、残念の極みであるが、上記のような事情を了とせられ、意のあるところをなにとぞお酌み取り頂きたい。
令和2年5月15日
元仙台高検検事長・平田胤明(たねあき)
元法務省官房長・堀田力
元東京高検検事長・村山弘義
元大阪高検検事長・杉原弘泰
元最高検検事・土屋守
同・清水勇男
同・久保裕
同・五十嵐紀男
元検事総長・松尾邦弘
元最高検公判部長・本江威憙(ほんごうたけよし)
元最高検検事・町田幸雄
同・池田茂穂
同・加藤康栄
同・吉田博視
(本意見書とりまとめ担当・文責)清水勇男
法務大臣 森まさこ殿
芥川龍之介が「蜘蛛の糸」を発表して百年。高二の秋の文化祭,クラスの仮装行列のテーマが 蜘蛛の糸だった。お釈迦様の極楽タワーの竹を近所から切り出し,地獄の焔と煙の絵を描いた。犍陀多に続いて蜘蛛の糸(登山部の赤いザイル)に群がる地獄の亡者だったころ。
2020年5月16日土曜日
2020年5月15日金曜日
オンライン授業ルーチン
今日で,オンライン授業の4回目のルーチンが終了した。古典力学(水2限,34名),科学のための数学(木2限,50名),電磁気学(金3限,42名)である。3科目だけでも連日めちゃくちゃ忙しいのであった。そのルーチンを整理すると次のようになる。
【オンライン授業ルーチンのまとめ】
◎事前の授業範囲の確定 1時間
①事前の課題の解答案作成,1〜2時間
②事前のノート+問題作成(5p)4〜6時間
③事前の5ページ分の音声収録 1〜2時間
④事前のファイル転送→mp4→OneDrive 1時間
⑤事前のmoodleサイトの編集+次回分 1時間
⑥当日の確認作業,レポート・質問収集 1時間
⑦当日のチャット 1〜2時間
⑧当日の成績表作成 1時間
⑨当日の質疑応答 1時間
⑩次回までの課題収集,質問確認 1〜2時間
もし,次年度も担当するのであれば,かなり負担が軽減されると思うが,残念なことに,非常勤は今年までなので,なんとも無駄なエネルギーを費やしている感がいなめない。
喜連川先生が司会している,国立情報学研究所の「4月からの大学等遠隔授業に関する取組状況共有サイバーシンポジウム」も連続して視聴しているが,全国的にたいへんな状況である。でも,新しい気付きもたくさんあるし,これによって,大学教育が本質的に見直される契機としてはよいかもしれない。9月入学にエネルギーを注いでいる場合ではない。今こそICTの活用に全力で取り組むべきなのだと思う今日この頃。20年前の「インターネットと教育」ブームは,結局は何の力にも成り得なかったとしても,この日につながっていることは間違いない。
[1]データダイエットへの協力のお願い:遠隔授業を主催される先生方へ(NII)
【オンライン授業ルーチンのまとめ】
◎事前の授業範囲の確定 1時間
①事前の課題の解答案作成,1〜2時間
②事前のノート+問題作成(5p)4〜6時間
③事前の5ページ分の音声収録 1〜2時間
④事前のファイル転送→mp4→OneDrive 1時間
⑤事前のmoodleサイトの編集+次回分 1時間
⑥当日の確認作業,レポート・質問収集 1時間
⑦当日のチャット 1〜2時間
⑧当日の成績表作成 1時間
⑨当日の質疑応答 1時間
⑩次回までの課題収集,質問確認 1〜2時間
もし,次年度も担当するのであれば,かなり負担が軽減されると思うが,残念なことに,非常勤は今年までなので,なんとも無駄なエネルギーを費やしている感がいなめない。
喜連川先生が司会している,国立情報学研究所の「4月からの大学等遠隔授業に関する取組状況共有サイバーシンポジウム」も連続して視聴しているが,全国的にたいへんな状況である。でも,新しい気付きもたくさんあるし,これによって,大学教育が本質的に見直される契機としてはよいかもしれない。9月入学にエネルギーを注いでいる場合ではない。今こそICTの活用に全力で取り組むべきなのだと思う今日この頃。20年前の「インターネットと教育」ブームは,結局は何の力にも成り得なかったとしても,この日につながっていることは間違いない。
[1]データダイエットへの協力のお願い:遠隔授業を主催される先生方へ(NII)
2020年5月14日木曜日
緊急事態宣言解除(1)
5月14日,全都道府県に出されていた新型コロナウイルス対策緊急事態宣言が,39県で解除された。この中には13の特定警戒都道府県のうち,茨城県,石川県,愛知県,岐阜県,福岡県を含んでいる。ということで,北海道,東京都,神奈川県,埼玉県,千葉県,大阪府,兵庫県,京都府はおあずけだ。
しかし,大阪府は独自のモデルによる出口戦略の7日間連続条件が満たされたとして,休業要請の段階的な解除をはじめた。これに関する吉村の説明力は,あべちゃんのレベルをはるかに越えているので,支持者が増えるわけだ。これが維新ののしあがる契機となるのだとしたら,歴史はなんとひどいことをしてくれたものだということになるのかもしれない。
しかし,大阪府は独自のモデルによる出口戦略の7日間連続条件が満たされたとして,休業要請の段階的な解除をはじめた。これに関する吉村の説明力は,あべちゃんのレベルをはるかに越えているので,支持者が増えるわけだ。これが維新ののしあがる契機となるのだとしたら,歴史はなんとひどいことをしてくれたものだということになるのかもしれない。
2020年5月13日水曜日
パトカー
駐車場の入口付近に放置自転車が2週間ほど滞在されていて,車の出し入れに不都合があるということで,駐車場のオーナーに1週間ほど前に連絡差し上げるも,状況が変化しなかったので,天理警察署に防犯登録番号と車体番号と事情を連絡したところ,早速パトカーで3名のマスク警察官が見に来て下さったのであるが,調べていただいた結果,盗難届は出ておらず所有者の電話番号も使われていないということで,あとは,駐車場の管理者に連絡して処分しもらって下さいという,ウェブで検索したようなご回答をいただいたのであり,こちらとしても,この忙しい時期にわざわざ出向いていただいたことに,手厚くお礼を申し上げながら,この案件が終了してしまった。チーン。
2020年5月12日火曜日
えっ,この非常時にさえICTを使わないのなぜ?
文部科学省の令和2年度ICT活用アドバイザー事業「学校の情報環境整備に関する説明会(当日資料)」が5月11日(月)に開催され,youtubeでも配信されていた。また,まさきとみずもとかづきさんによるnoteで一部(重要な部分)が文字おこしされている。
文部科学省初等中等教育局情報教育・外国語教育課長の髙谷浩樹さんの説明はなかなか気合いが入っていた。配布資料にはなかったが,以下の部分がキモでした。
これからはICTを使わないことに説明責任が伴う(地方自治体に向けて),説明責任が伴うのは本件の文部科学省の私であり地方教育行政をになうあなた達である。我々は一蓮托生なのである。今までが間違っていたのだ。やろうとしないのは子どもに対する罪である。
豊福晋平さんは辛口のコメントをしていたが,みんながんばってほしい。
文部科学省初等中等教育局情報教育・外国語教育課長の髙谷浩樹さんの説明はなかなか気合いが入っていた。配布資料にはなかったが,以下の部分がキモでした。
図 高谷課長の声が聞こえてきた
豊福晋平さんは辛口のコメントをしていたが,みんながんばってほしい。
2020年5月11日月曜日
ヨビノリ(2)
ヨビノリ(1)からの続き
去年この記事を書いたのは教育系YouTuberがちょっと話題になっていたころだった。今日は,ヨビノリたくみさんが,2020年の2月14日に文部科学省で開かれた政策立案教養研修で講演しているYou Tube番組に行き当たった。なかなか参考になった。
この時点でのチャンネル登録者が30万人(その3ヶ月後の現在は42.5万人に達しているのだ。新型コロナウイルス感染症がもたらすオンライン教育への地殻変動の大きさがわかる),動画本数が400本,平均再生回数13万回/日,総再生回数3300万回(今日の時点では5000万回近くになっている)。
大学の理系学部の授業のシラバスに掲載され,参考資料としての活用が促されているようだ。また,視聴者層は,中高生20%,大学生・大学院生40%,社会人40%となっている。先端研究者(大学教員)へのインタビューや,ノーベル賞の説明など,幅広くこのニッチ市場を開拓している。また,ヨビノリはヨビノリたくみ+ヨビノリやすで構成されていたことをあらためて認識した。
自分でオンライン授業のためのノート+音声の紙芝居コンテンツを毎日3科目分つくってみると,ヨビノリコンテンツがさすがによくできていることを改めて感じることになった今日この頃。
去年この記事を書いたのは教育系YouTuberがちょっと話題になっていたころだった。今日は,ヨビノリたくみさんが,2020年の2月14日に文部科学省で開かれた政策立案教養研修で講演しているYou Tube番組に行き当たった。なかなか参考になった。
この時点でのチャンネル登録者が30万人(その3ヶ月後の現在は42.5万人に達しているのだ。新型コロナウイルス感染症がもたらすオンライン教育への地殻変動の大きさがわかる),動画本数が400本,平均再生回数13万回/日,総再生回数3300万回(今日の時点では5000万回近くになっている)。
大学の理系学部の授業のシラバスに掲載され,参考資料としての活用が促されているようだ。また,視聴者層は,中高生20%,大学生・大学院生40%,社会人40%となっている。先端研究者(大学教員)へのインタビューや,ノーベル賞の説明など,幅広くこのニッチ市場を開拓している。また,ヨビノリはヨビノリたくみ+ヨビノリやすで構成されていたことをあらためて認識した。
自分でオンライン授業のためのノート+音声の紙芝居コンテンツを毎日3科目分つくってみると,ヨビノリコンテンツがさすがによくできていることを改めて感じることになった今日この頃。
2020年5月10日日曜日
検察庁法改正案に反対する
twitterでのハッシュタグ署名「#検察庁法改正案に抗議します」が380万件を越えたようだ(NHK 2020.5.10 17:00ごろの記事にて※)。
森友−加計−桜などの一連の流れの総決算で,自民−公明−維新が国会の強行突破を図っている。ひどい話である。制度としても非常に大きな問題をかかえてしまう。
検察庁法は検察庁の組織と検察官の任免の手続きを定めている。今回の改正案は,国家公務員法等の一部を改正する法律案の中にあって,その問題点のキモは,「役職定年を導入し,検事正については法務大臣の判断,次長検事および検事長については内閣の判断で,個別に役職定年を延長することができるようにしたところ(なお,現在の検察庁法には役職定年の制度はない)」のようだ。
※その後400万件を越えたあたりで, https://twittrend.jp からは消されてしまったようだ。あいかわらず,twitter.jpの恣意的・政治的な運営は本当にひどいことになっている。その痕跡が図の地域別の一部に残っているという指摘があった。
[1]検事長の勤務延長に関する閣議決定の撤回を求め、国家公務員法等の一部を改正する法律案に反対する会長声明|あらためて検察庁法の一部改正に反対する会長声明(日本弁護士連合会)
[2]我が国の検察制度の特色(検察庁)
[3]いったい検察庁法改正案の何に抗議しているのか(徐東輝)
[4]安倍首相による 検察,警察の私物化−新型コロナ危機の陰で進む民主主義・法の支配の崩壊(小西洋之)
[5]「#検察庁法改正案に抗議します」をめぐって知っておいてほしいこと(山尾志桜里)
[6]twittrend(各地域のついっトレンド)
[7]twitter trending hashtag (こちらは改竄されておらず,約550万件に到達)
森友−加計−桜などの一連の流れの総決算で,自民−公明−維新が国会の強行突破を図っている。ひどい話である。制度としても非常に大きな問題をかかえてしまう。
検察庁法は検察庁の組織と検察官の任免の手続きを定めている。今回の改正案は,国家公務員法等の一部を改正する法律案の中にあって,その問題点のキモは,「役職定年を導入し,検事正については法務大臣の判断,次長検事および検事長については内閣の判断で,個別に役職定年を延長することができるようにしたところ(なお,現在の検察庁法には役職定年の制度はない)」のようだ。
第四条 検察庁法(昭和二十二年法律第六十一号)の一部を次のように改正する。などのあたりだろうか。
・・・
法務大臣は、前項の規定にかかわらず、年齢が六十三年に達した検事正の職を占める検事について、当該検事の職務の遂行上の特別の事情を勘案して、当該検事を他の職に補することにより公務の運営に著しい支障が生ずると認められる事由として法務大臣が定める準則(以下この条において単に「準則」という。)で定める事由があると認めるときは、当該検事が年齢六十三年に達した日の翌日から起算して一年を超えない範囲内で期限を定め、引き続き当該検事に、当該検事が年齢六十三年に達した日において占めていた職を占めたまま勤務をさせることができる。
法務大臣は、前項の期限又はこの項の規定により延長した期限が到来する場合において、前項の事由が引き続きあると認めるときは、準則で定めるところにより、これらの期限の翌日から起算して一年を超えない範囲内(その範囲内に定年に達する日がある検事にあつては、延長した期限の翌日から当該定年に達する日までの範囲内)で期限を延長することができる。
・・・
内閣は、前項の規定にかかわらず、年齢が六十三年に達した次長検事又は検事長について、当該次長検事又は検事長の職務の遂行上の特別の事情を勘案して、当該次長検事又は検事長を検事に任命することにより公務の運営に著しい支障が生ずると認められる事由として内閣が定める事由があると認めるときは、当該次長検事又は検事長が年齢六十三年に達した日の翌日から起算して一年を超えない範囲内で期限を定め、引き続き当該次長検事又は検事長に、当該次長検事又は検事長が年齢六十三年に達した日において占めていた官及び職を占めたまま勤務をさせることができる。
内閣は、前項の期限又はこの項の規定により延長した期限が到来する場合において、前項の事由が引き続きあると認めるときは、内閣の定めるところにより、これらの期限の翌日から起算して一年を超えない範囲内(その範囲内に定年に達する日がある次長検事又は検事長にあつては、延長した期限の翌日から当該定年に達する日までの範囲内)で期限を延長することができる。
図 twitterndにみられるtwitter改竄の痕跡?(左ビフォアー,右アフター)
※その後400万件を越えたあたりで, https://twittrend.jp からは消されてしまったようだ。あいかわらず,twitter.jpの恣意的・政治的な運営は本当にひどいことになっている。その痕跡が図の地域別の一部に残っているという指摘があった。
[1]検事長の勤務延長に関する閣議決定の撤回を求め、国家公務員法等の一部を改正する法律案に反対する会長声明|あらためて検察庁法の一部改正に反対する会長声明(日本弁護士連合会)
[2]我が国の検察制度の特色(検察庁)
[3]いったい検察庁法改正案の何に抗議しているのか(徐東輝)
[4]安倍首相による 検察,警察の私物化−新型コロナ危機の陰で進む民主主義・法の支配の崩壊(小西洋之)
[5]「#検察庁法改正案に抗議します」をめぐって知っておいてほしいこと(山尾志桜里)
[6]twittrend(各地域のついっトレンド)
[7]twitter trending hashtag (こちらは改竄されておらず,約550万件に到達)
2020年5月9日土曜日
ハナノナ
このところCOVID-19の話ばかり書いてきたのでちょっと食傷気味である。
今日は別の話題です。「無料でカメラを向けた花の名前を即座にAIが教えてくれるアプリハナノナを使ってみた」という記事があったのでさっそくiPhoneにインストールしたところ,なかなかすごいのだった。ベランダのムラサキカタバミを早速言い当てた。
千葉工業大学のステアラボ(人工知能・ソフトウェア技術研究センター)で2017年に開発されたものらしい。ウエブサービスハナノナとして始まった。最近,認識できる花の種類のが770種類にまでアップデートされ,iPhoneアプリも登場した。この手のアプリはのどから手が出るほどほしかった。まあ,ないことはなかったのです。これまでに,京都大学発祥?のいきものコレクションアプリBIOMEを使ったこともあるのだけれど,機能を欲張りすぎた割には精度がいまいちで,アプリ画面のこやしになっていた。
その点,ハナノナは単純な機能がよいのである(草木にも拡張してほしい)。この調子でトリノナ(鳥類),ムシノナ(節足動物・両生類・爬虫類),クモノナ(雲です),ホシノナ(☆です),イシノナ(岩石鉱物),トモノナ(ホ乳類),ウオノナ(魚類・水生生物)など作っていただけるとうれしいなあ。これらができた後でモノノナ(万物)に統合されるのはOKです。これで小学校の理科はOKです。
今日は別の話題です。「無料でカメラを向けた花の名前を即座にAIが教えてくれるアプリハナノナを使ってみた」という記事があったのでさっそくiPhoneにインストールしたところ,なかなかすごいのだった。ベランダのムラサキカタバミを早速言い当てた。
千葉工業大学のステアラボ(人工知能・ソフトウェア技術研究センター)で2017年に開発されたものらしい。ウエブサービスハナノナとして始まった。最近,認識できる花の種類のが770種類にまでアップデートされ,iPhoneアプリも登場した。この手のアプリはのどから手が出るほどほしかった。まあ,ないことはなかったのです。これまでに,京都大学発祥?のいきものコレクションアプリBIOMEを使ったこともあるのだけれど,機能を欲張りすぎた割には精度がいまいちで,アプリ画面のこやしになっていた。
その点,ハナノナは単純な機能がよいのである(草木にも拡張してほしい)。この調子でトリノナ(鳥類),ムシノナ(節足動物・両生類・爬虫類),クモノナ(雲です),ホシノナ(☆です),イシノナ(岩石鉱物),トモノナ(ホ乳類),ウオノナ(魚類・水生生物)など作っていただけるとうれしいなあ。これらができた後でモノノナ(万物)に統合されるのはOKです。これで小学校の理科はOKです。
図 本日の朝の散歩におけるハナノナの成果の一部(2020.5.9撮影)
追伸:モノノナのイメージが出てきた。目に映るものの名前をできる限り知りたい(デイリーポータル,2020.05.22)
2020年5月8日金曜日
小田垣さんのSIQR
朝日新聞に,九州大学名誉教授の小田垣さんの計算として「PCR検査を倍にすれば、接触「5割減」でも収束可能?」という記事がでた。twitterでも注目を集めていた。
小田垣さんのホームページにその論考があった[1]。SIQRモデルということで,感染者を2段階に分けていた。我々のSIIDR2モデルと本質的に同じではないか。感受性保持者S(t)から直接我々の重症患者I2(t),すなわち小田垣さんの隔離感染者Q(t)に遷移する項があって,ここは違うのだが,議論が始まる前の段階でこの項を落としているので結局同じです。違うのはこちらには死亡数D(t)への遷移を含んでいることくらいである。
そこで両方のモデルで使用しているパラメタを比較してみた。左が小田垣さんのSIQR,右が我々のSIIDR2である。
\begin{equation}
\begin{aligned}
N\beta \quad (0.07) &= \beta \quad (0.4-0.6) \\
p \quad (0.096) &= \dfrac{1}{\alpha_2} \quad (0.04) \\
\gamma \quad (0.04) &= \dfrac{1}{\alpha_1} \quad (0.16) \\
\gamma \quad (0.04) &= \dfrac{1}{\gamma_1}\quad (0.064) \\
noparameter (0) &= \dfrac{1}{\gamma_2}\quad (0.00267) \\
\end{aligned}
\end{equation}
感染率の$\beta$が一桁違うことがわかる。その他はファクターが異なるくらいである。I(t)からR(t)への遷移時間とQ(t)からR(t)への遷移時間が同じとしていることもやや疑問に感じる。また,小田垣氏は論考の中で,基本再生産数(実効再生産数)は$N\beta/p$でなく$N\beta/(p+\gamma)$とすべきだと主張しているが,これはどうなのだろうか。
とりあえず,感染初期のS(t)=Nのときにあてはめて,接触5割減の議論に持ち込んでいる部分は興味深いが,実際にこのパラメータを使って日本の感染データの全体像を説明できるのだろうか。我々のコードを少し修正して彼らのモデルとパラメタを使った計算を再現してみた(初期値の細かな調整は我々のモデルを前提としているがとりあえずはそこはそのままにしておく)。
- - - - - - - - - - - - - - - - - - - - - - - - - - - - -
using DifferentialEquations
using ParameterizedFunctions
using Plots; gr()
sky = @ode_def SIQR_model begin
du0 = 1 # u0:time
du1 = -β*u1*u2/n # u1:Noimmunity(Susceptible)
du2 = β*u1*u2/n -u2/α2 -u2/α1 # u2:(Infected)
du3 = u2/α2 -u3/γ1 # u3:(Quarantined)
du4 = u3/γ2 # u4:Dead(not in use)
du5 = u2/α1 +u3/γ1 # u5:Recovered
du6 = u2/α2 # u6:Accumulated Quarantined
du7 = u3/γ1 # u7:Accululated Recovered
end n α1 α2 β γ1 γ2 λ τ
function epidm(β,ν,λ,τ,T)
n=10000.0 #total number of population
α1=1/0.04 #5.0/0.8 #latent to recovery (days/%)
α2=1/0.096 #5.0/0.2 #latent to onset (days/%)
β=0.07 #0.45 #infection rate (/day・person)
γ1=1/0.04 #15.0/0.96 #onset to recovery (days/%)
γ2=15.0/0.04 #onset to death (days/%) (not in use)
u0 = [0.0,n-11ν,4ν,2ν,0.0,5ν,ν,0.0] #initial values
p = (n,α1,α2,β,γ1,γ2,λ,τ) #parameters
tspan = (0.0,T) #time span in days
prob = ODEProblem(sky,u0,tspan,p)
sol = solve(prob)
return sol
end
#japan-data(start=3/1)
xj=[0,1,2,3,4,5,6,7,8,9,10,11,12,13,
14,15,16,17,18,19,20,21,22,23,24,25,26,27,
28,29,30,31,32,33,34,35,36,37,38,39,40,41,
42,43,44,45,46,47,48,49,50,51,52,53,54,55,
56,57,58,59,60,61,62]
yj=[0.0190,0.0202,0.0213,0.0225,0.0252,0.0277,0.0324,
0.0361,0.0387,0.0408,0.0451,0.0492,0.0536,0.0568,
0.0619,0.0646,0.0658,0.0658,0.0693,0.0754,0.0790,
0.0830,0.0864,0.0895,0.0947,0.103,0.110,0.119,
0.134,0.148,0.155,0.173,0.189,0.208,0.232,
0.260,0.290,0.310,0.338,0.378,0.424,0.477,
0.536,0.576,0.607,0.643,0.681,0.728,0.777,
0.822,0.853,0.882,0.912,0.946,0.983,1.018,
1.046,1.062,1.078,1.099,1.118,1.133,1.154]
zj=[0.040,0.048,0.048,0.048,0.048,0.048,0.048,
0.048,0.056,0.071,0.095,0.119,0.151,0.167,
0.175,0.190,0.222,0.222,0.230,0.262,0.278,
0.286,0.325,0.333,0.341,0.357,0.365,0.389,
0.413,0.429,0.444,0.452,0.452,0.516,0.548,
0.556,0.579,0.635,0.643,0.675,0.698,0.746,
0.778,0.810,0.865,0.944,1.079,1.175,1.222,
1.278,1.357,1.476,2.198,2.278,2.516,2.651,
2.762,2.786,2.984,3.087,3.294,3.429,3.603]/100
plot(xj,yj,st=:scatter,label="Confirmed-japan")
#plot!(xj,zj,st=:scatter,label="Deaths-japan")
β=0.07
ν=0.01
T=60
@time so=epidm(β,ν,λ,τ,T)
#plot!(so,vars=(0,2))
#plot!(so,vars=(0,3))
plot!(so,vars=(0,4))
#plot!(so,vars=(0,5))
#plot!(so,vars=(0,6))
plot!(so,vars=(0,7))
- - - - - - - - - - - - - - - - - - - - - - - - - - - - -
[1]新型コロナウイルスの蔓延に関する一考察(小田垣孝,2020.5.5)
[2]隔離と市中の感染者を分ける SIR モデル(佐野雅己,2020.4.29)
[3]3.11以後の科学リテラシー No. 89(牧野淳一郎,2020 科学5月号)
[4]感染症の数理シミュレーション(8)(2020.3.15)
小田垣さんのホームページにその論考があった[1]。SIQRモデルということで,感染者を2段階に分けていた。我々のSIIDR2モデルと本質的に同じではないか。感受性保持者S(t)から直接我々の重症患者I2(t),すなわち小田垣さんの隔離感染者Q(t)に遷移する項があって,ここは違うのだが,議論が始まる前の段階でこの項を落としているので結局同じです。違うのはこちらには死亡数D(t)への遷移を含んでいることくらいである。
そこで両方のモデルで使用しているパラメタを比較してみた。左が小田垣さんのSIQR,右が我々のSIIDR2である。
\begin{equation}
\begin{aligned}
N\beta \quad (0.07) &= \beta \quad (0.4-0.6) \\
p \quad (0.096) &= \dfrac{1}{\alpha_2} \quad (0.04) \\
\gamma \quad (0.04) &= \dfrac{1}{\alpha_1} \quad (0.16) \\
\gamma \quad (0.04) &= \dfrac{1}{\gamma_1}\quad (0.064) \\
noparameter (0) &= \dfrac{1}{\gamma_2}\quad (0.00267) \\
\end{aligned}
\end{equation}
感染率の$\beta$が一桁違うことがわかる。その他はファクターが異なるくらいである。I(t)からR(t)への遷移時間とQ(t)からR(t)への遷移時間が同じとしていることもやや疑問に感じる。また,小田垣氏は論考の中で,基本再生産数(実効再生産数)は$N\beta/p$でなく$N\beta/(p+\gamma)$とすべきだと主張しているが,これはどうなのだろうか。
とりあえず,感染初期のS(t)=Nのときにあてはめて,接触5割減の議論に持ち込んでいる部分は興味深いが,実際にこのパラメータを使って日本の感染データの全体像を説明できるのだろうか。我々のコードを少し修正して彼らのモデルとパラメタを使った計算を再現してみた(初期値の細かな調整は我々のモデルを前提としているがとりあえずはそこはそのままにしておく)。
- - - - - - - - - - - - - - - - - - - - - - - - - - - - -
using DifferentialEquations
using ParameterizedFunctions
using Plots; gr()
sky = @ode_def SIQR_model begin
du0 = 1 # u0:time
du1 = -β*u1*u2/n # u1:Noimmunity(Susceptible)
du2 = β*u1*u2/n -u2/α2 -u2/α1 # u2:(Infected)
du3 = u2/α2 -u3/γ1 # u3:(Quarantined)
du4 = u3/γ2 # u4:Dead(not in use)
du5 = u2/α1 +u3/γ1 # u5:Recovered
du6 = u2/α2 # u6:Accumulated Quarantined
du7 = u3/γ1 # u7:Accululated Recovered
end n α1 α2 β γ1 γ2 λ τ
function epidm(β,ν,λ,τ,T)
n=10000.0 #total number of population
α1=1/0.04 #5.0/0.8 #latent to recovery (days/%)
α2=1/0.096 #5.0/0.2 #latent to onset (days/%)
β=0.07 #0.45 #infection rate (/day・person)
γ1=1/0.04 #15.0/0.96 #onset to recovery (days/%)
γ2=15.0/0.04 #onset to death (days/%) (not in use)
u0 = [0.0,n-11ν,4ν,2ν,0.0,5ν,ν,0.0] #initial values
p = (n,α1,α2,β,γ1,γ2,λ,τ) #parameters
tspan = (0.0,T) #time span in days
prob = ODEProblem(sky,u0,tspan,p)
sol = solve(prob)
return sol
end
#japan-data(start=3/1)
xj=[0,1,2,3,4,5,6,7,8,9,10,11,12,13,
14,15,16,17,18,19,20,21,22,23,24,25,26,27,
28,29,30,31,32,33,34,35,36,37,38,39,40,41,
42,43,44,45,46,47,48,49,50,51,52,53,54,55,
56,57,58,59,60,61,62]
yj=[0.0190,0.0202,0.0213,0.0225,0.0252,0.0277,0.0324,
0.0361,0.0387,0.0408,0.0451,0.0492,0.0536,0.0568,
0.0619,0.0646,0.0658,0.0658,0.0693,0.0754,0.0790,
0.0830,0.0864,0.0895,0.0947,0.103,0.110,0.119,
0.134,0.148,0.155,0.173,0.189,0.208,0.232,
0.260,0.290,0.310,0.338,0.378,0.424,0.477,
0.536,0.576,0.607,0.643,0.681,0.728,0.777,
0.822,0.853,0.882,0.912,0.946,0.983,1.018,
1.046,1.062,1.078,1.099,1.118,1.133,1.154]
zj=[0.040,0.048,0.048,0.048,0.048,0.048,0.048,
0.048,0.056,0.071,0.095,0.119,0.151,0.167,
0.175,0.190,0.222,0.222,0.230,0.262,0.278,
0.286,0.325,0.333,0.341,0.357,0.365,0.389,
0.413,0.429,0.444,0.452,0.452,0.516,0.548,
0.556,0.579,0.635,0.643,0.675,0.698,0.746,
0.778,0.810,0.865,0.944,1.079,1.175,1.222,
1.278,1.357,1.476,2.198,2.278,2.516,2.651,
2.762,2.786,2.984,3.087,3.294,3.429,3.603]/100
plot(xj,yj,st=:scatter,label="Confirmed-japan")
#plot!(xj,zj,st=:scatter,label="Deaths-japan")
β=0.07
ν=0.01
T=60
@time so=epidm(β,ν,λ,τ,T)
#plot!(so,vars=(0,2))
#plot!(so,vars=(0,3))
plot!(so,vars=(0,4))
#plot!(so,vars=(0,5))
#plot!(so,vars=(0,6))
plot!(so,vars=(0,7))
- - - - - - - - - - - - - - - - - - - - - - - - - - - - -
結果は以下の通りである。確かに初期の段階ではデータを説明しているが,その後の振る舞いは説明できない。このモデル(のパラメタ)はあまりよろしくないのかもしれない。
[1]新型コロナウイルスの蔓延に関する一考察(小田垣孝,2020.5.5)
[2]隔離と市中の感染者を分ける SIR モデル(佐野雅己,2020.4.29)
[3]3.11以後の科学リテラシー No. 89(牧野淳一郎,2020 科学5月号)
[4]感染症の数理シミュレーション(8)(2020.3.15)
2020年5月7日木曜日
中野さんのK値
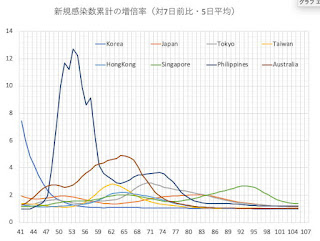
阪大の杉山清寛さんのFacebookから,RCNPの中野貴志さん(ペンタクオークでおなじみ)がCOVID-19の収束状況を判定するK値というのを考案しているという情報がみつかった。あれ,こちらで計算していたものと本質的に同じ量ではないか。彼のK値は次式で与えられる[2]。総感染者数は我々の(というか普通報道されている)新規感染数累計(Confirmed)のことだ。3月の末に,新規感染数累計の増倍率という記事[1]を書いていた(忘れていた)。
K = 1 - (1週間前の総感染者数) / (当日の総感染者数)
こちらで計算を続けていたのは,r = (当日の総感染者数)/ (1週間前の総感染者数) = 1/(1-K) である。最近1に収束してきて(下に有界な単調減少数列)おもしろい情報がとれないので更新を停止したところであった。なるほど,こうすれば,初期段階の感度は悪いが,収束段階の感度はよくなる。また,中野さんの最近の論考[3]ではさらに考察が進化していた。まあ,物理屋さんがやるとだいたいこういう発想になるのだろう。
その3月下旬から4月にかけて日本だけが他の国と違う振る舞いを見せていてどきどきしたが,やがて収まった。逆にシンガポールの異常を発見したのもこれを観察していたときだった。
[1]新規感染数累計の増倍率(2020.3.31)
[2]COVID-19 感染状況の推移について(中野貴志,2020.4.19)
[3]K 値で読み解く COVID-19 の感染状況と今後の推移(中野貴志・池田陽一,2020.5.6)
[4]新型コロナウイルス感染症(COVID-19)について(吉森保,2020.5.10)
K = 1 - (1週間前の総感染者数) / (当日の総感染者数)
こちらで計算を続けていたのは,r = (当日の総感染者数)/ (1週間前の総感染者数) = 1/(1-K) である。最近1に収束してきて(下に有界な単調減少数列)おもしろい情報がとれないので更新を停止したところであった。なるほど,こうすれば,初期段階の感度は悪いが,収束段階の感度はよくなる。また,中野さんの最近の論考[3]ではさらに考察が進化していた。まあ,物理屋さんがやるとだいたいこういう発想になるのだろう。
図1 アジアの新規感染数累計増倍率の推移(2020.3.1-5.4)
図2 ヨーロッパの新規感染数累計増倍率の推移(2020.3.9-5.4)
その3月下旬から4月にかけて日本だけが他の国と違う振る舞いを見せていてどきどきしたが,やがて収まった。逆にシンガポールの異常を発見したのもこれを観察していたときだった。
[1]新規感染数累計の増倍率(2020.3.31)
[2]COVID-19 感染状況の推移について(中野貴志,2020.4.19)
[3]K 値で読み解く COVID-19 の感染状況と今後の推移(中野貴志・池田陽一,2020.5.6)
[4]新型コロナウイルス感染症(COVID-19)について(吉森保,2020.5.10)
2020年5月6日水曜日
米国の集団免疫率(3)
米国の集団免疫率(2)からの続き
タイトルはもう変更したほうがいいかもしれない。というのも,抗体検査の結果,ニューヨーク州では12.3%が抗体を持っている(感染済)という結果がでているからだ。こちらの結果とはほぼ1桁違うので,我々のモデルの前提や仮定のどれかががまったく間違っているのではないか。しかし,モデルを検討する余力がないので(遠隔授業の準備で手いっぱい),そこは放置したまま,米国の新しいデータに基づいたパラメタ推定を行う。というのも,これまでの6万人から6.5万人という発表に代わり,再び死亡者が10万人を越えるという予想が出ているからだ。前回と同様に,HEMLのCOVID-19 projections のページを見れば,確かに米国全体の死亡数は8月には13.4万人になりそうだとある。
前回同様のSIIDR2モデルで計算する。使用するWHOのデータ(人口1万人当り)はこれ。
- - - - - - - - - - - - - - - - - - - - - - - - - - - - -
ya=[0.014,0.021,0.030,0.038,0.051,0.051,0.051,
0.106,0.107,0.215,0.317,0.462,0.462,0.958,
1.280,1.576,1.929,2.074,2.587,3.136,3.722,
4.268,4.953,5.684,6.483,7.335,8.310,9.327,
10.13,11.03,11.99,12.93,14.00,14.96,15.92,
16.81,17.55,18.33,19.20,20.19,21.10,21.96,
22.80,23.58,24.31,25.19,26.12,27.29,28.28,
29.16,29.85,30.47,31.42,32.39,33.20,34.16]
za=[0.0006,0.0008,0.0009,0.0011,0.0012,0.0012,0.0012,
0.0018,0.0018,0.0030,0.0046,0.0061,0.0061,0.0122,
0.0143,0.0204,0.0268,0.0301,0.0377,0.0506,0.0641,
0.0728,0.0865,0.117,0.146,0.178,0.213,0.254,
0.290,0.329,0.387,0.445,0.504,0.562,0.620,
0.667,0.712,0.785,0.856,0.922,0.984,1.038,
1.089,1.141,1.216,1.284,1.337,1.402,1.456,
1.492,1.532,1.591,1.679,1.742,1.792,1.842]
- - - - - - - - - - - - - - - - - - - - - - - - - - - - -
P. S. 日本でも,神戸の病院の外来患者の約3%に新型コロナウイルス感染症の抗体が検出されたとある。なかなか大きな数字だ。これが1%だとしても,大都市部の数十万人が感染済みということ。
タイトルはもう変更したほうがいいかもしれない。というのも,抗体検査の結果,ニューヨーク州では12.3%が抗体を持っている(感染済)という結果がでているからだ。こちらの結果とはほぼ1桁違うので,我々のモデルの前提や仮定のどれかががまったく間違っているのではないか。しかし,モデルを検討する余力がないので(遠隔授業の準備で手いっぱい),そこは放置したまま,米国の新しいデータに基づいたパラメタ推定を行う。というのも,これまでの6万人から6.5万人という発表に代わり,再び死亡者が10万人を越えるという予想が出ているからだ。前回と同様に,HEMLのCOVID-19 projections のページを見れば,確かに米国全体の死亡数は8月には13.4万人になりそうだとある。
前回同様のSIIDR2モデルで計算する。使用するWHOのデータ(人口1万人当り)はこれ。
- - - - - - - - - - - - - - - - - - - - - - - - - - - - -
ya=[0.014,0.021,0.030,0.038,0.051,0.051,0.051,
0.106,0.107,0.215,0.317,0.462,0.462,0.958,
1.280,1.576,1.929,2.074,2.587,3.136,3.722,
4.268,4.953,5.684,6.483,7.335,8.310,9.327,
10.13,11.03,11.99,12.93,14.00,14.96,15.92,
16.81,17.55,18.33,19.20,20.19,21.10,21.96,
22.80,23.58,24.31,25.19,26.12,27.29,28.28,
29.16,29.85,30.47,31.42,32.39,33.20,34.16]
za=[0.0006,0.0008,0.0009,0.0011,0.0012,0.0012,0.0012,
0.0018,0.0018,0.0030,0.0046,0.0061,0.0061,0.0122,
0.0143,0.0204,0.0268,0.0301,0.0377,0.0506,0.0641,
0.0728,0.0865,0.117,0.146,0.178,0.213,0.254,
0.290,0.329,0.387,0.445,0.504,0.562,0.620,
0.667,0.712,0.785,0.856,0.922,0.984,1.038,
1.089,1.141,1.216,1.284,1.337,1.402,1.456,
1.492,1.532,1.591,1.679,1.742,1.792,1.842]
- - - - - - - - - - - - - - - - - - - - - - - - - - - - -
パラメタはこれ,前回と少し変えている。
#β=0.61,ν=0.12,λ=49,τ=16,α2=5.0/0.20,γ2†=15.0/0.10
結果はこれ,確かに15〜16万人くらいになりそうだ。
図 米国の感染カーブ(u3=重症感染数,u4=死亡数,u6=新規感染数累計,1万人当)
2020年5月5日火曜日
CFR(致命率)(1)
一つの集団におけるある感染症の致命率(Case Fatality Rate)とは,その集団における感染者数に対する,その感染症が原因となる死亡者数の比率である。COVID-19における各国の致命率の時間推移が次のサイトMotality Risk of COVID-19 (Our World in Data)にある。そこでいくつかの代表的な国々を選んで図示してみた。
図 各国のCFRの推移(3/20-5/2)
アジアが欧米に比べて明らかに低いのは何故かという問題提起があったが,これをみれば,米国と中国は同じオーダーである。ここに載せていない,台湾,香港,シンガポールが非常に小さいのは確かである。
2020年5月4日月曜日
新型コロナ感染症の時系列
自分で計算できる実効再生産数からの続き
高橋健太郎さんが12日シフトで説明できるということだったので,これまでの経緯を時系列でまとめ,前回の実効再生産数の計算値の日付を12日だけ引き算した日時にあてはめてならべてみたものを,日付[数値]として埋め込んだ表を作った。
- - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
1/30 新型コロナウイルス感染症対策本部の設置
2/04 ダイヤモンドプリンセス横浜で再検疫
2/16 [1.0]
2/19 ダイヤモンドプリンセス下船開始
2/21 [2.1]
2/26 全国的イベント自粛(Perfume EXILE)
2/29 [1.1]
3/01 ダイヤモンドプリンセス全員下船
2/28 北海道知事の緊急事態宣言
3/02 要請に基づく全国学校休業(-春休み)
3/05 [1.0]
3/08 大相撲無観客場所初日
3/13 [2.1]
3/14 新型インフルエンザ等対策特別措置法改正
3/17 特措法にもとづく新型コロナウイルス感染症対策本部へ
3/20 [1.7]
3/24 東京五輪を2021年に延期
3/25 東京都重要局面発言/春休み
3/28 [1.5]
3/29 志村けん
3/31 [1.0]
4/05 [1.0]
4/07 7都府県に特措法による緊急事態宣言(-5/6)
4/16 [0.5]
4/16 全国に特措法による緊急事態宣言(-5/6)
5/04 全国の緊急事態宣言延長(-5/31)
- - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
高橋健太郎さんが12日シフトで説明できるということだったので,これまでの経緯を時系列でまとめ,前回の実効再生産数の計算値の日付を12日だけ引き算した日時にあてはめてならべてみたものを,日付[数値]として埋め込んだ表を作った。
- - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
1/30 新型コロナウイルス感染症対策本部の設置
2/04 ダイヤモンドプリンセス横浜で再検疫
2/16 [1.0]
2/19 ダイヤモンドプリンセス下船開始
2/21 [2.1]
2/26 全国的イベント自粛(Perfume EXILE)
2/29 [1.1]
3/01 ダイヤモンドプリンセス全員下船
2/28 北海道知事の緊急事態宣言
3/02 要請に基づく全国学校休業(-春休み)
3/05 [1.0]
3/08 大相撲無観客場所初日
3/13 [2.1]
3/14 新型インフルエンザ等対策特別措置法改正
3/17 特措法にもとづく新型コロナウイルス感染症対策本部へ
3/20 [1.7]
3/24 東京五輪を2021年に延期
3/25 東京都重要局面発言/春休み
3/28 [1.5]
3/29 志村けん
3/31 [1.0]
4/05 [1.0]
4/07 7都府県に特措法による緊急事態宣言(-5/6)
4/16 [0.5]
4/16 全国に特措法による緊急事態宣言(-5/6)
5/04 全国の緊急事態宣言延長(-5/31)
- - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
細かいところまで対応させて解釈するのはきびしいかもしれない。
[1]新型コロナウイルス(COVID-19)への正しい理解をするためのオンライン学習教材について(島根県立出雲高等学校,大日康史・菅原民枝)
[1]新型コロナウイルス(COVID-19)への正しい理解をするためのオンライン学習教材について(島根県立出雲高等学校,大日康史・菅原民枝)
2020年5月3日日曜日
自分で計算できる実効再生産数
新型コロナウイルス感染症専門家会議が5月1日に出した提言・状況分析における実効再生産数のグラフについてあれこれいわれている。こういう場合は自分で確かめておよその感じをつかみたい。いやいやこんな緊急事態に素人が世情を惑わせるよけいな計算をしてはいけないという声も,かつてよけいなことをしまくったその分野の素人(別の分野の専門家)から聞こえてくるのである。ここでComputational Thinkingを標榜するのであれば,計算の自由(Freedom of Computation)を宣言しておきたい。もちろんそのためには最低限データとアルゴリズムを明らかにしておく必要がある(専門家会議はそうしていない)。
①使用するデータ:日本の新規感染数の日次統計(WHOに報告されたもの)WHOのSituation Reportsのデータ(確定感染者数 Confirmed)は次のようになった。ただし,2月22日から5月1日まで(WHOが公表している日付を基準としたもの)の70点のデータである。
{12,27,12,13,7,22,24,20,9,15,14,16,33,32,59,48,33,26,54,52,55,41,64,34,15,15,44,77,46,50,43,39,65,98,96,112,194,173,87,225,206,233,303,351,383,252,351,511,579,658,743,507,390,455,482,585,628,566,390,367,378,423,469,441,353,203,191,276,236,193}
②使用するモデル:単純なSIRモデルを仮定し,感染が人口の数%を越えて拡がっていないものとし,未感染者数(感受性保持者 Susceptible $S(t)$)が全人口($N$ 定数)とほぼ等しいとする。なお,感染者(Infected $I(t)$)と未感染者の接触による1人1日当りの感染率 $\beta$は対策効果を含めて時間の関数$\beta(t)$とした。さらに,感染期間(日)を$\alpha$として,実効再生産数を$R_t=\alpha \beta(t)$で定義する。このとき,感染者数$I(t)$は次の微分方程式を満足し,$R_t$は$I(t)$とその時間微分から求まる。
\begin{equation}
\begin{aligned}
\dfrac{d I(t) }{dt} = \beta(t) S(t) I(t) / N - I(t) / \alpha \approx \dfrac{ R_t - 1}{ \alpha} I(t) \\
\therefore R_t = 1 + \alpha \dfrac{d I(t) }{dt} / I(t)
\end{aligned}
\end{equation}
③計算方法:誤差はあるけれど時間の単位を1日とする差分式に直して,エクセルで計算する。もとの新規感染数データのままではゆらぎが大きいので,5日移動平均を求めて$I(t)$とする。これから中心差分($I(t+1)-I(t-1))/2$)で1日当りの新規感染数の変化分を求める。さらに,このゆらぎを緩和するためにこの5日移動平均をもとめて$d I(t)$とする。これから②の式を用いて$R_t$を求めた。
④結果:図のとおりである。
[3]感染症数理モデル(北海道大学医学統計学教室のSqquential SEIRモデル)
[4]Rt-COVID-19 Japan (都道府県別新型コロナウイルスの実効再生産数)
[5]山中伸弥による新型コロナウイルス情報発信
[6]A New Framework and Software to Estimate Time-Varying Reproduction Numbers During Epidemics(Cori et al.)
[7]新型コロナ対策専門家会議が判断の拠り所にしている『実効再生産数・倍加時間』の算出方法に関する考察(@makirin1230 2020.05.06)
①使用するデータ:日本の新規感染数の日次統計(WHOに報告されたもの)WHOのSituation Reportsのデータ(確定感染者数 Confirmed)は次のようになった。ただし,2月22日から5月1日まで(WHOが公表している日付を基準としたもの)の70点のデータである。
{12,27,12,13,7,22,24,20,9,15,14,16,33,32,59,48,33,26,54,52,55,41,64,34,15,15,44,77,46,50,43,39,65,98,96,112,194,173,87,225,206,233,303,351,383,252,351,511,579,658,743,507,390,455,482,585,628,566,390,367,378,423,469,441,353,203,191,276,236,193}
②使用するモデル:単純なSIRモデルを仮定し,感染が人口の数%を越えて拡がっていないものとし,未感染者数(感受性保持者 Susceptible $S(t)$)が全人口($N$ 定数)とほぼ等しいとする。なお,感染者(Infected $I(t)$)と未感染者の接触による1人1日当りの感染率 $\beta$は対策効果を含めて時間の関数$\beta(t)$とした。さらに,感染期間(日)を$\alpha$として,実効再生産数を$R_t=\alpha \beta(t)$で定義する。このとき,感染者数$I(t)$は次の微分方程式を満足し,$R_t$は$I(t)$とその時間微分から求まる。
\begin{equation}
\begin{aligned}
\dfrac{d I(t) }{dt} = \beta(t) S(t) I(t) / N - I(t) / \alpha \approx \dfrac{ R_t - 1}{ \alpha} I(t) \\
\therefore R_t = 1 + \alpha \dfrac{d I(t) }{dt} / I(t)
\end{aligned}
\end{equation}
③計算方法:誤差はあるけれど時間の単位を1日とする差分式に直して,エクセルで計算する。もとの新規感染数データのままではゆらぎが大きいので,5日移動平均を求めて$I(t)$とする。これから中心差分($I(t+1)-I(t-1))/2$)で1日当りの新規感染数の変化分を求める。さらに,このゆらぎを緩和するためにこの5日移動平均をもとめて$d I(t)$とする。これから②の式を用いて$R_t$を求めた。
④結果:図のとおりである。
図1 全国の新規感染数の推移(2/22-5/1)
図2 全国の実効再生産数の推移(2/24-4/29)
図2には社会的な事象を書き加えているが,WHOへの報告公表時点とは時間的なずれ(1週間〜10日)があることに注意する。→(注)12日ぐらいか(P. S. 参照)
⑤ 結論:1ヶ月前に1.5〜2.0近くまであった$R_t$が現在0.5〜1.0の範囲にまで落ちてきたことがみてとれ,これは専門家会議の結果とおおよそ近いものである。しかし,細かく見ればそのピークの位置や高さは異なっている。とくに,2月末から3月中旬までの結果は待ったく違う。そもそも出発点となる新規感染数のデータもWHOに報告されたものは,1週間の大きな周期構造を持っており,牧野さんのいうように(ちょっと意味が違うかもしれないけれど),専門家会議が確定感染者数(Confirmed)からどのように処理して新規感染数の推定値を導いているのかがはっきりしないのでもやもやが残る。
P. S. 高橋健太郎さん(@kentarotakahash)によれば,「潜伏期間+発症〜報告までの日数の平均を12日と考えてみたら、かなり納得できました。15日目あたりから一度、下降してRe=1を切りますが、2/24+15-12ですので、2月27日の休校要請の効果に見えます。その下降のピークは3月4日頃。一週間で緩んで、再び上昇が始まった。3月10日頃にRe=2を越えるピーク。」だそうだ。またさらに,「その後、Re=1.5以上の状態が続きますが、三連休の人手の反省があり、3月25日の都知事緊急記者会見を経て、3月27日頃から下降に転じる。3月31日にはRe=1を切り、専門家会議の4月1日には1を下回ったという分析と合致します。」
そして,「その後一度、上昇して、1を越えますが、4月5日頃から本格的な下降が始まる。これは緊急事態宣言が出るというムードの先取り。が、4月14日あたりから再び上昇の兆しというところでしょうか。」なるほどなのだった。
[1]新型コロナウイルス感染症対策専門家会議の見解等(牧野淳一郎,2020.04.18)
[2]新型コロナウイルス感染症対策専門家会議の見解等その2(牧野淳一郎,2020.05.12)[3]感染症数理モデル(北海道大学医学統計学教室のSqquential SEIRモデル)
[4]Rt-COVID-19 Japan (都道府県別新型コロナウイルスの実効再生産数)
[5]山中伸弥による新型コロナウイルス情報発信
[6]A New Framework and Software to Estimate Time-Varying Reproduction Numbers During Epidemics(Cori et al.)
[7]新型コロナ対策専門家会議が判断の拠り所にしている『実効再生産数・倍加時間』の算出方法に関する考察(@makirin1230 2020.05.06)
2020年5月2日土曜日
WHOのSituation reports
WHOがCOVID-19の特設ページで毎日掲載しているSituation reportsの様式が,5月1日版から模様替えした。なんでもいいからCSVで出してほしい。日本の厚生労働省とかわらないのか。
これまでは,もとのpdfファイルから,pdftotext(コマンドラインツール)でテキストにしたものと, PDFelement6 Pro(無料版)でエクセル化したものとを組み合わせて,国・地域別データを整理した日次統計テキストファイルをつくっていた。
新しい様式ではpdftotextの出力がちょっとましな感じだったので,perlプログラミング1発+若干の手作業による修正で,上記の日次統計テキストファイルまでたどり着くことができそうだ。
いや,Johns Hopkins 大学のCSVデータを使えという話もあるかもしれないが,いちおうそこはほれ,WHOを支持しているので。
あいかわらず正規表現もまともに習得していないので泥臭いperlプログラムになった。
- - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
- - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
※WHOのデータ形式が変わったので,若干修正した(2020.5.7)。
これまでは,もとのpdfファイルから,pdftotext(コマンドラインツール)でテキストにしたものと, PDFelement6 Pro(無料版)でエクセル化したものとを組み合わせて,国・地域別データを整理した日次統計テキストファイルをつくっていた。
新しい様式ではpdftotextの出力がちょっとましな感じだったので,perlプログラミング1発+若干の手作業による修正で,上記の日次統計テキストファイルまでたどり着くことができそうだ。
いや,Johns Hopkins 大学のCSVデータを使えという話もあるかもしれないが,いちおうそこはほれ,WHOを支持しているので。
あいかわらず正規表現もまともに習得していないので泥臭いperlプログラムになった。
- - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
# /usr/local/bin/perl
# 05/02/2020 K. Koshigiri
# 05/07/2020 K. Koshigiri -> revised version
# 05/07/2020 K. Koshigiri -> revised version
# extract data from WHO covid-19 reports
# https://www.who.int/emergencies/diseases/
# novel-coronavirus-2019/situation-reports/
# usage:: ./who.pl < pdf-in.txt > out.txt
while($line = <STDIN>) {
chomp($line);
if($line =~ /([A-Z].*)/) {
$a=$1;
$a =~ s/\(.*//;
$flg='a';
} elsif($flg eq 'a' && $line =~ /([\d\h]+)/) {
$b=$1;
$b =~ s/\h//;
$flg='b';
} elsif($flg eq 'b' && $line =~ /([\d\h]+)/) {
$c=$1;
$c =~ s/\h//;
$flg='c';
} elsif($flg eq 'c' && $line =~ /([\d\h]+)/) {
$d=$1;
$d =~ s/\h//;
$flg='d';
} elsif($flg eq 'd' && $line =~ /([\d\h]+)/) {
$e=$1;
$e =~ s/\h//;
$flg='';
print("$a\n$b\n$c\n$d\n$e\n");
}
}
※WHOのデータ形式が変わったので,若干修正した(2020.5.7)。
2020年5月1日金曜日
実効再生産数
新型コロナウイルス感染症対策専門家会議が5月1日の発表で実効再生産数$R_t$の値を示していた。だいぶ前に東京で$R_t$=1.7という数字を出して以来,この値については沈黙していたので,あちこちから不満があがっていたためかもしれない。
図 全国の実効再生産数の値(朝日新聞から引用)
新規感染数のピークが600人を越えていないのは何故だろう。生データや簡単な移動平均では600人を越えると思う。また,推定感染者数となってため,減少期の振動構造も消えているのだろうか。
2020年4月30日木曜日
新規感染数の推移
5月6日が期限であった全国の緊急事態宣言が1ヶ月程度延長されそうであまり異論はないようにみえる。twitterで各国の新規感染数を比較しながらこの問題を検討している人がいた。自分でもやってみた。ただし時間軸は揃え,イタリア,英国,日本×5,スウェーデン×5を試しにやってみる。
図 新規感染数の推移(3/12-4/29)(日本とスウェーデンは5倍した値)
日本のデータが信頼性に欠けているということはさんざん指摘されている。それでもなお日本は,英国の高止まりやスウェーデンの上昇傾向とは異なりイタリアのような下降線に近いようにみえてしまう。本当のところはどうなのだろうか。まだ予断を許さない。
2020年4月29日水曜日
9月入学
どうやら5月6日に緊急事態宣言を解除するのは難しいとわかってきて,目くらましと先延ばしと人気取りのために9月入学を声高に叫び始める維新や国民民主や首長たち。下手すると経産官邸族に唆されてアベノマスク氏も乗ってしまうのかもしれない。やめたほうがいいような気がするけど。やっぱり入学式には桜がないといけませんね。COVID-19の次の波がきたらまた半年づつずらすのかよ。東大が失敗した大学だけシフトはありうるとは思うけれど・・・。子どもたちの学習保障はそれはそれで別に考えるほうがよいと思う。このたいへんで不確定要因が多い時期に更なる混乱を招くだけだろう。むしろ,各大学が入試問題を従来のように作れるのか,大学院入試ができるのか,などが老婆心ながら気になるところ。
2020年4月28日火曜日
東京タワーとスカイツリー
テレビで(テレビの見過ぎ),東京タワーと東京スカイツリーが同じ高さにみえる場所を探すというのがあった。その場所を結ぶ軌跡は円になっていた。そうなのか。
原点に高さ$h_1$の塔を置き,$x=a\ (a>0)$の点に高さ$h_2\ (>h_1)$の塔を置く。$x$軸上には仰角が等しくなる点が2つあり,$x/h_1 = (a-x)/h_2$と$x/h_1 = (a+x)/h_2$を満たす点であり,$x=\frac{a}{1 \pm h_2/h_1}$ で与えられる。
次に点P $(x,y)$を考えて,この点からの仰角が等しくなるための条件を求めれば,
\begin{equation}
\dfrac{x^2+y^2}{h_1^2} = \dfrac{(a-x)^2+y^2}{h_2^2}
\end{equation}
である。整理すれば以下のように円の方程式が得られる。ここで,無次元の量 $c$を $c=(h_2/h_1)^2-1$と置いた。
\begin{equation}
\begin{aligned}
\bigl\{ ( h_2 / h_1 )^2 - 1 \bigr\} x^2 + 2 a x + \bigl\{ ( h_2 / h_1 )^2 - 1 \bigr\} y^2 = a^2 \\
(x + a/c)^2+y^2=a^2/c *\bigl( 1 + 1/c \bigr) = (a/c * h_2/h_1)^2
\end{aligned}
\end{equation}
中心の位置は先ほど$x$軸上に求めた2点の中点になっている。円の半径は$a/c * h_2/h_1$である。
原点に高さ$h_1$の塔を置き,$x=a\ (a>0)$の点に高さ$h_2\ (>h_1)$の塔を置く。$x$軸上には仰角が等しくなる点が2つあり,$x/h_1 = (a-x)/h_2$と$x/h_1 = (a+x)/h_2$を満たす点であり,$x=\frac{a}{1 \pm h_2/h_1}$ で与えられる。
次に点P $(x,y)$を考えて,この点からの仰角が等しくなるための条件を求めれば,
\begin{equation}
\dfrac{x^2+y^2}{h_1^2} = \dfrac{(a-x)^2+y^2}{h_2^2}
\end{equation}
である。整理すれば以下のように円の方程式が得られる。ここで,無次元の量 $c$を $c=(h_2/h_1)^2-1$と置いた。
\begin{equation}
\begin{aligned}
\bigl\{ ( h_2 / h_1 )^2 - 1 \bigr\} x^2 + 2 a x + \bigl\{ ( h_2 / h_1 )^2 - 1 \bigr\} y^2 = a^2 \\
(x + a/c)^2+y^2=a^2/c *\bigl( 1 + 1/c \bigr) = (a/c * h_2/h_1)^2
\end{aligned}
\end{equation}
中心の位置は先ほど$x$軸上に求めた2点の中点になっている。円の半径は$a/c * h_2/h_1$である。
2020年4月27日月曜日
有界な単調数列は収束する
大人の学び直し
- - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
○実数を項とする無限数列 $\{a_n\}$ を考える。すなわち,$n \in \mathbb{N}$,$a_n \in \mathbb{R}$ である。数列 $\{a_n\}$ の全ての項を要素とする集合を $A$ とする。すなわち,$A=\{a_1, a_2, a_3, \dots \}$ である。
○集合 $X$ が 上に(下に)有界 であるとは,$\forall x \in X \rightarrow x \le (\ge) M$ となる実数 $M$ が存在することである。この $M$ を $X$ の上界(下界) とよぶ。$X$ が上にも下にも有界であれば,$X$ は 有界 であるという。
○上界(下界)$M$ が $M\in X$ であるとき,これを $X$ の 最大値(最小値) という。
○上界(下界)の集合が空集合 $\emptyset$ でないとき,上界(下界)の最小値を $X$ の上限(下限) という。空集合ならば,上限(下限)を $\infty \ (-\infty)\ $ と表すことがある。
○なお,数列 $\{a_n\}$ については,その全ての項からなる集合 $A$ についての表現を流用して,数列に対して,有界,上界(下界),最大値(最小値),上限(下限)などの用語をあてはめることにする。
○数列 $\{a_n\}$ が有界ならば,$\forall n \in \mathbb{N} \rightarrow |a_n| \le M$ と表すことができる。
○数列 $\{a_n\}$ が 単調増加(減少) であるとは,すべての$n \in \mathbb{N}$に対して,$a_n \le a_{n+1}\ ( a_n \ge a_{n+1} )\ $ が成立することである。等号を含めない場合は, 狭義単調増加(減少) であるという。単調増加と単調減少の性質を持つ数列をまとめて 単調数列 という。
○数列が収束する ことは次のように表現する。各項が実数である無限数列 $\{a_n\}$ がある。この数列が実数 $\alpha$ に収束するとは,つぎの関係が成り立つことをいう。『任意の $\varepsilon > 0$ に対して,ある自然数 $N(\varepsilon)$ が存在して,$n \ge N(\varepsilon)$ をみたす 任意の自然数 $n$ について $| a_n - \alpha | < \varepsilon $をみたす』
$\forall \varepsilon > 0,\ \exists N(\varepsilon) \in \mathbb {N} \ \mathrm{s.t.}\ \forall n \in \mathbb {N} \quad [\ n \ge N(\varepsilon) \Rightarrow | a_{n} - \alpha | < \varepsilon \ ]$
○「 有界な単調数列は収束する 」を証明するための前提としては,実数に関する次の公理が必要となる。すなわち,「上に(下に)有界な実数の部分集合には最小上界(最大下界)が存在する。」
○証明は次のように進む。上に(下に)有界な数列 $\{a_n\}$ があるとすると,その最小上界(最大下界)を $\alpha$ とすると,すべての $n$ に対して,$a_n \le \alpha \ (a_n \ge \alpha)\ $ が成り立つ。
○ 最小上界より小さな数(最大下界より大きな数) $\alpha \mp \varepsilon \ ( \varepsilon > 0 )\ $を考えると,この数と $\alpha$ との間には数列 $\{a_n\}$ の部分が存在する(存在しなければ, $\alpha$ が最小上界や最大下界ではないことになるから)。つまり,$\varepsilon$ を与えると定まる自然数 $N$ が存在し,それは,$a_N > \alpha -\varepsilon \ ( a_N < \alpha + \varepsilon )\ $を満足する。
○$\{a_n\}$ は単調増加(単調減少)数列なので,$n \ge N$ となる $n$ に対して,$a_n \ge a_N > \alpha -\varepsilon \ (a_n \le a_N < \alpha + \varepsilon)\ $である。一方,$a_n \le \alpha \ ( a_n \ge \alpha )\ $ より,$a_n < \alpha + \varepsilon \ (a_n > \alpha - \varepsilon )\ $ である。
○これらより,$n \ge N$ となるすべての $n$ に対して,$ |a_n - \alpha | < \varepsilon $ が成り立つ。したがって,数列 $\{a_n\}$ は $\alpha$ に収束する。これを次式のように表して,$\alpha$ を収束する数列の 極限値 という。
$\lim_{n \to \infty} a_n = \alpha$
2020年4月26日日曜日
COVID-19雑感(2)
昨日のものを再編してみた。
○ニューヨーク州の抗体検査による既感染累計が人口の14%というのはほんとうだろうか。
(もしそうならモデルパラメタの前提がそもそも間違っている)
○スウェーデンの試み(ロックダウンしない)は成功するのだろうか。死亡数累計が人口の0.02%を越えて増加中である。スペインの0.04%よりは小さいが,増加率が・・・
○ブラジル,ロシアなどもじわじわと増えている。
○ニューヨーク州の抗体検査による既感染累計が人口の14%というのはほんとうだろうか。
(もしそうならモデルパラメタの前提がそもそも間違っている)
○スウェーデンの試み(ロックダウンしない)は成功するのだろうか。死亡数累計が人口の0.02%を越えて増加中である。スペインの0.04%よりは小さいが,増加率が・・・
○ブラジル,ロシアなどもじわじわと増えている。
図 欧州・米州の新規感染数累計の推移(人口の10ppm時点を原点)
2020年4月25日土曜日
COVID-19雑感(1)
徒然なるままに・・・
○日本は相変わらず情緒的な対処法で乗り切ろうとしている。正確なデータがないままに。
○シンガポールの新規感染数累計は,人口比で0.2%となり湖北省の0.1%を越えた。まだ収まる様子がみえないのだけれど大丈夫かしら(それにしては死亡数累計が少ない)。
○東京は,韓国・オーストラリアを越えてまだ収束先がみえない。日本全体も上昇中。
(残念なことに,石川県と福井県が人口比で東京についで2位と3位なのだ)
○台湾,中国,韓国,香港は,第1段階が終息している。
○通常のインフルエンザと比較して問題なしとする正論?は正しいのだろうか。
○日本は相変わらず情緒的な対処法で乗り切ろうとしている。正確なデータがないままに。
○シンガポールの新規感染数累計は,人口比で0.2%となり湖北省の0.1%を越えた。まだ収まる様子がみえないのだけれど大丈夫かしら(それにしては死亡数累計が少ない)。
○東京は,韓国・オーストラリアを越えてまだ収束先がみえない。日本全体も上昇中。
(残念なことに,石川県と福井県が人口比で東京についで2位と3位なのだ)
○台湾,中国,韓国,香港は,第1段階が終息している。
○通常のインフルエンザと比較して問題なしとする正論?は正しいのだろうか。
図 アジア・太平洋の新規感染数累計の推移(人口の10ppm時点を原点)
2020年4月24日金曜日
原子核の周期表
京大の萩野浩一さんと前野悦輝さんが,原子核の周期表を考案し,三次元化したモデルを「ニュークリタッチ」(元素の周期表の三次元モデル「エレメンタッチ」の仲間)と命名したとの発表が京都大学からあった。
論文のほうは,A Nuclear Periodic Table で,Foundations of Chemistry に発表される。
いやー,かつてのシェルモデルユーザとしては盲点でしたね。なかなかおもしろく,教育的な価値もあると思う。
論文のほうは,A Nuclear Periodic Table で,Foundations of Chemistry に発表される。
いやー,かつてのシェルモデルユーザとしては盲点でしたね。なかなかおもしろく,教育的な価値もあると思う。
2020年4月23日木曜日
遠隔授業のばたばた(6)
遠隔授業のばたばた(5)からの続き
今日は1回生の「科学のための数学」の初回である。昨日は主に2回生でmoodleにも慣れている集団だったが,今日はどうだろうか。
受講登録者52名の内,45名が出席チェックを通過,46名がアンケートをクリアした。
自宅が44名,寮・下宿が1名,その他(どこやねん)が1名。デスクトップPCが1名,スマホが4名,41名がノートPCである。50GB程度は速度制限なしに利用できるが2名,上記より小さいかわからないが3名,41名が自宅のネットワークなどで無制限に利用できる。まあだいたい昨日と同じ傾向だった。
なお,高等学校で数Ⅲを履修していないものが,11名/46名と1/4あるので毎年のように授業の進め方が難しい。全員化学を選択しているが,物理は35名,生物は13名といったところ。
練習課題の提出でひとり手間取った。手順は次の通りである。
① スマホなどで課題を撮影した写真を PC に取り込む。
② PowerPoint に上記写真ファイルを貼る。
③ 写真を選択した状態で,書式→図の圧縮 または 図の書式設定→圧縮 を実行する。
(最小のメールサイズにして下さい)
④この PowerPoint ファイルを koshigiri-k-0420.pptx のように名前を付けて保存。
⑤ koshigiri-k-0420.pptx を pdf ファイルとして出力し moodle の課題提出箱に提出する。
これをチャットで手取り足取り教えることになった。なかなかハードルの高い道のりである。
今日は1回生の「科学のための数学」の初回である。昨日は主に2回生でmoodleにも慣れている集団だったが,今日はどうだろうか。
受講登録者52名の内,45名が出席チェックを通過,46名がアンケートをクリアした。
自宅が44名,寮・下宿が1名,その他(どこやねん)が1名。デスクトップPCが1名,スマホが4名,41名がノートPCである。50GB程度は速度制限なしに利用できるが2名,上記より小さいかわからないが3名,41名が自宅のネットワークなどで無制限に利用できる。まあだいたい昨日と同じ傾向だった。
なお,高等学校で数Ⅲを履修していないものが,11名/46名と1/4あるので毎年のように授業の進め方が難しい。全員化学を選択しているが,物理は35名,生物は13名といったところ。
練習課題の提出でひとり手間取った。手順は次の通りである。
① スマホなどで課題を撮影した写真を PC に取り込む。
② PowerPoint に上記写真ファイルを貼る。
③ 写真を選択した状態で,書式→図の圧縮 または 図の書式設定→圧縮 を実行する。
(最小のメールサイズにして下さい)
④この PowerPoint ファイルを koshigiri-k-0420.pptx のように名前を付けて保存。
⑤ koshigiri-k-0420.pptx を pdf ファイルとして出力し moodle の課題提出箱に提出する。
これをチャットで手取り足取り教えることになった。なかなかハードルの高い道のりである。
2020年4月22日水曜日
遠隔授業のばたばた(5)
遠隔授業のばたばた(4)からの続き
いよいよから今日から自分の最初の授業「古典力学(前期水曜2限)」が始まった。とりあえず用意したものは,moodleのページとOneDriveに置いた音声付きノート3ページ(各10分≒10MB)である。
moodleのページの段取りは以下の通りである(学生は自己登録でゲストアカウントも可にしている)。学年暦の都合で次回は今週の土曜日にやってくる。
- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
第1回 オリエンテーション(4/22水)
学生からの質問箱
質問や意見はこちらにどうぞ。
第1回出席チェック
出席チェックが終わったら受講生アンケートに進んで下さい。
受講生アンケート
受講生アンケートが終わったらチャットルームを試して下さい。
第1回チャットルーム
授業時間中はここでも質疑応答を受けます。
第1回の講義内容
この中のファイルを視聴して下さい。
練習課題の提出ボックス
練習課題を本日中に提出して下さい。
練習課題「ノートに自分の学籍番号と名前,今日の感想(数行)を書いたものを撮影し,pdfファイルにして提出する」
第1回の課題を提出
第1回課題は次回(4/25土)までに提出してください。
- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
10時半をすぎると出席チェックが増え出した。結局36名の受講者全員が出席チェックしている。チャットルームはほとんどみんな通りすぎていく。質問が2,3件あった。
アンケートは匿名であったがほぼ解答している。通信環境不明が2名,5G以下が3名,50G以下が1名,他は無制限だ。受講場所は,寮・下宿が3名で,他は自宅だ。端末はスマホが8名,タブレットが1名,デスクトップPCが1名,他はノートPCだ。高校で数Ⅲを履修していないものが6名いた。
練習課題がなかなか集まらない。授業終了の12時ごろで1/3,13時をまわったところでようやく半数だったので,moodleのアナウンスメントを使って全員にメールによるお知らせをして,困った場合は申し出るようにする。
まあ,第1回なので評判はそこそこであった。しかし準備にかなりの時間がとられてしまうのが難点である。このままいつまで続けられることだろうか。でも,授業としてはこの形態のほうが望ましいとも思えた。反転授業に大きくかじ取りすべきかもしれない。
P. S. 夕方,zoomによる全学説明会があった。オンライン授業は5月末まで延長というか,実技・実験・実習科目以外は基本オンライン授業でということだ。問題は,中国留学生,期末試験,実習などだろうか。いまのところmoodleの負荷問題は深刻化していない。
いよいよから今日から自分の最初の授業「古典力学(前期水曜2限)」が始まった。とりあえず用意したものは,moodleのページとOneDriveに置いた音声付きノート3ページ(各10分≒10MB)である。
moodleのページの段取りは以下の通りである(学生は自己登録でゲストアカウントも可にしている)。学年暦の都合で次回は今週の土曜日にやってくる。
- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
第1回 オリエンテーション(4/22水)
学生からの質問箱
質問や意見はこちらにどうぞ。
第1回出席チェック
出席チェックが終わったら受講生アンケートに進んで下さい。
受講生アンケート
受講生アンケートが終わったらチャットルームを試して下さい。
第1回チャットルーム
授業時間中はここでも質疑応答を受けます。
第1回の講義内容
この中のファイルを視聴して下さい。
練習課題の提出ボックス
練習課題を本日中に提出して下さい。
練習課題「ノートに自分の学籍番号と名前,今日の感想(数行)を書いたものを撮影し,pdfファイルにして提出する」
第1回の課題を提出
第1回課題は次回(4/25土)までに提出してください。
- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
アンケートは匿名であったがほぼ解答している。通信環境不明が2名,5G以下が3名,50G以下が1名,他は無制限だ。受講場所は,寮・下宿が3名で,他は自宅だ。端末はスマホが8名,タブレットが1名,デスクトップPCが1名,他はノートPCだ。高校で数Ⅲを履修していないものが6名いた。
練習課題がなかなか集まらない。授業終了の12時ごろで1/3,13時をまわったところでようやく半数だったので,moodleのアナウンスメントを使って全員にメールによるお知らせをして,困った場合は申し出るようにする。
まあ,第1回なので評判はそこそこであった。しかし準備にかなりの時間がとられてしまうのが難点である。このままいつまで続けられることだろうか。でも,授業としてはこの形態のほうが望ましいとも思えた。反転授業に大きくかじ取りすべきかもしれない。
P. S. 夕方,zoomによる全学説明会があった。オンライン授業は5月末まで延長というか,実技・実験・実習科目以外は基本オンライン授業でということだ。問題は,中国留学生,期末試験,実習などだろうか。いまのところmoodleの負荷問題は深刻化していない。
2020年4月21日火曜日
ウルフラムの物理
Stephan Wolfram の "A Class of Models with the Potential to Represent Fundamental Physics" がarxiv.orgに投稿されていた。440ページもあるぞ。
1. Introduction
2. Basic Form of Models
3. Typical Behaviors
4. Limiting Behavior and Emergent Geometry
5. The Updating Process for String Substitution Systems
6. The Updating Process in Our Models
7. Equivalence and Computation in Our Models
8. Potential Relation to Physics
Additional Material
References
発売予定のハードカバー,A Project to Find the Fundamental Theory of Physics(816ページ)のドラフトかと思ったけれど,そうではなかった。WolframのA New Kind of Science から続いている思想の延長線上にある。たぶん,大学に入る前に新聞でカタストロフィーの理論をみて,わーこれはすごい!と思ったが,実際のところはそうでもなくてちょっと残念だったのに近いのではないかと予想しているのだけれど。それでもちょっとワクワクする。
A class of models intended to be as minimal and structureless as possible is introduced. Even in cases with simple rules, rich and complex behavior is found to emerge, and striking correspondences to some important core known features of fundamental physics are seen, suggesting the possibility that the models may provide a new approach to finding a fundamental theory of physics.
可能な限り最小で構造のないモデルのクラスが紹介されている。単純なルールの場合でも,豊かで複雑な振る舞いが現れることがわかり、基礎物理学の重要な核となる既知の特徴との顕著な対応が見られ、このモデルが物理学の基礎理論を見つけるための新しいアプローチを提供する可能性を示唆している。目次は次のとおりである。
1. Introduction
2. Basic Form of Models
3. Typical Behaviors
4. Limiting Behavior and Emergent Geometry
5. The Updating Process for String Substitution Systems
6. The Updating Process in Our Models
7. Equivalence and Computation in Our Models
8. Potential Relation to Physics
Additional Material
References
発売予定のハードカバー,A Project to Find the Fundamental Theory of Physics(816ページ)のドラフトかと思ったけれど,そうではなかった。WolframのA New Kind of Science から続いている思想の延長線上にある。たぶん,大学に入る前に新聞でカタストロフィーの理論をみて,わーこれはすごい!と思ったが,実際のところはそうでもなくてちょっと残念だったのに近いのではないかと予想しているのだけれど。それでもちょっとワクワクする。
[1]A Class of Models with the Potential to Represent Fundamental Physics(上記のオンラインバージョン)
2020年4月20日月曜日
遠隔授業のばたばた(4)
遠隔授業のばたばた(3)からの続き
4月20日,いよいよ今日からはじまった。ただ,こちらから観測されている範囲では大きなトラブルはない。教務システムUNIPAも学習管理システムmoodleも無事に動いているようだ。もっとも,現場は学生からの質問で大わらわ状態のようだが。
現時点でmoodleに登録されている授業で検索にかかった主なものは下記のとおり。
1限 2限 3限 4限 5限 6限 7限 合計
月曜 14 18 23 16 5 8 4 88
火曜 13 23 18 18 3 5 6 86
水曜 10 17 0 1 0 5 4 37
木曜 10 28 26 16 4 1 4 89
金曜 13 21 19 17 6 2 3 81
合計 60 107 86 68 18 21 21 381
うーん,大丈夫なのだろうか。
4月20日,いよいよ今日からはじまった。ただ,こちらから観測されている範囲では大きなトラブルはない。教務システムUNIPAも学習管理システムmoodleも無事に動いているようだ。もっとも,現場は学生からの質問で大わらわ状態のようだが。
現時点でmoodleに登録されている授業で検索にかかった主なものは下記のとおり。
1限 2限 3限 4限 5限 6限 7限 合計
月曜 14 18 23 16 5 8 4 88
火曜 13 23 18 18 3 5 6 86
水曜 10 17 0 1 0 5 4 37
木曜 10 28 26 16 4 1 4 89
金曜 13 21 19 17 6 2 3 81
合計 60 107 86 68 18 21 21 381
うーん,大丈夫なのだろうか。
2020年4月19日日曜日
遠隔授業のばたばた(3)
遠隔授業のばたばた(2)からの続き
大阪府立大学の講義動画作成法のYouTubeがなかなか参考になった。田崎晴明さん方式 にしようかどうしようか。そこで,各種方法をまとめてみると次のようになる。
P. S. 課題の画像ファイル(2MB)は,PowerPointに貼り付けて画像圧縮(メールサイズ)にしてpdf出力すれば,100KBのオーダーに抑えることができた。
大阪府立大学の講義動画作成法のYouTubeがなかなか参考になった。田崎晴明さん方式 にしようかどうしようか。そこで,各種方法をまとめてみると次のようになる。
- 講師動画&板書動画(1ファイル)(300MB/45分)
- 講師音声&板書動画(1ファイル)(200MB/45分)
- 講師音声&ノート画像(1ファイル)(100MB/45分)
- 講師音声,ノート画像(2ファイル)(10MB/45分)
- zoomの講義録画 → a
- zoomの画面共有録画 → b
- QuickTimeの録画機能 → c
- PowerPoint/Keynoteの録画機能 → c
- iOSの録音機能+手書きアプリ → d (→ c FFmpegで編集:50MB/45分)
むしろ問題は学生からの課題回収のほうである。大学からはmoodleサーバ保護の観点から,テキストなどなるべく軽いデータで課題を出させよとのお達しがきた。A4プリント1枚の解答をスマホの写真で撮れば2MB程度になるので,50人のクラスでは100MB/授業1回となる。2000クラスで15回の授業を行えば3TBとなる。うーん,なかなか微妙なラインではある。写真をpdf化することに負担もあってどうしたものか思案のしどころ。
(こんなことばかりしていて肝腎の授業ノートが1ミリも進んでいない・・・orz)
P. S. 課題の画像ファイル(2MB)は,PowerPointに貼り付けて画像圧縮(メールサイズ)にしてpdf出力すれば,100KBのオーダーに抑えることができた。
2020年4月18日土曜日
遠隔授業のばたばた(2)
遠隔授業のばたばた(1)からの続き
今日も朝からmoodle支援を2件すませた。昼からは国立情報学研究所(NII)の【第4回】4月からの大学等遠隔授業に関する取組状況共有サイバーシンポジウム(4/17オンライン開催)に大阪教育大学の尾崎君が登場するようなので,さっそくアクセスすべくCiscoのWebexやブラウザエクステンションをインストールするなどの準備を行う。
画質と音質はだいぶ落としていたけれど,内容はかなりおもしろかった。とくに尾崎君の「オンライン授業実施に向けた個別サポートデスクの実施体制の構築とその運用」は,実用的でシンプルで汎用性も高いので,喜連川先生もほめていた。
そんなわけで,昨日に続いて試行錯誤が続いている。神戸高校の杉木勝彦先生(大阪教育大学理科教育専攻物理の稲垣研出身)が,遠隔授業用の教材作成に取り組んでいる。iPadのGoodnotesで作成した静止画に,コントロールセンターで有効にした画面収録機能を使って,音声を重ねるというものである。まず,ターゲットとなるノートを開いた状態でコントロールセンターを呼び出して画面収録をオンにする。説明のお話が終わったところで録画中ボタンをタッチして終了する。これにより写真のところに収録された動画がmp4形式で保存された(毎分7.5MB程度か)。
もう少し軽くならないかと検索しまくったところ,FFmegを使って,静止画と音声ファイルから動画を作るというのがあった。四苦八苦してあれこれ試したところ次のようにするとうまくいくことがわかった。結城浩さんのおかげである。
静止画(img.jpg)と音声ファイル(snd.m4a,iPhoneのボイスメモで収録)を使って,mp4ファイルを作るには次のようにする(-pix_fmt yuv420pがミソだった)。
ffmpeg -loop 1 -i img.jpg -i snd.m4a -ab 24k -vb 72k -c:v libx264 -pix_fmt yuv420p -shortest out.mp4
また,2つのmp4ファイルを結合するには次のようにする。
ffmpeg -safe 0 -f concat -i mylist.txt -c copy out3.mp4
ただし,mylist.txtには結合前のファイルを並べておけば良い。
cat mylist.txt (out?.mp4は同じコーデックで作ったファイルであること)
file ./out1.mp4
file ./out2.mp4
あとはコンテンツだ。熊本大学の鈴木克明さん(昔,日本文教出版の高等学校の情報の洋教科書でいろいろお世話になった。今,日本教育工学会の会長になっておられた)が上のシンポジウムで指摘していたように,無理せずにゆるゆると真の目的を見据えながらやるのがよろしいようだ。
遠隔授業のばたばた(3)に続く
今日も朝からmoodle支援を2件すませた。昼からは国立情報学研究所(NII)の【第4回】4月からの大学等遠隔授業に関する取組状況共有サイバーシンポジウム(4/17オンライン開催)に大阪教育大学の尾崎君が登場するようなので,さっそくアクセスすべくCiscoのWebexやブラウザエクステンションをインストールするなどの準備を行う。
画質と音質はだいぶ落としていたけれど,内容はかなりおもしろかった。とくに尾崎君の「オンライン授業実施に向けた個別サポートデスクの実施体制の構築とその運用」は,実用的でシンプルで汎用性も高いので,喜連川先生もほめていた。
そんなわけで,昨日に続いて試行錯誤が続いている。神戸高校の杉木勝彦先生(大阪教育大学理科教育専攻物理の稲垣研出身)が,遠隔授業用の教材作成に取り組んでいる。iPadのGoodnotesで作成した静止画に,コントロールセンターで有効にした画面収録機能を使って,音声を重ねるというものである。まず,ターゲットとなるノートを開いた状態でコントロールセンターを呼び出して画面収録をオンにする。説明のお話が終わったところで録画中ボタンをタッチして終了する。これにより写真のところに収録された動画がmp4形式で保存された(毎分7.5MB程度か)。
もう少し軽くならないかと検索しまくったところ,FFmegを使って,静止画と音声ファイルから動画を作るというのがあった。四苦八苦してあれこれ試したところ次のようにするとうまくいくことがわかった。結城浩さんのおかげである。
静止画(img.jpg)と音声ファイル(snd.m4a,iPhoneのボイスメモで収録)を使って,mp4ファイルを作るには次のようにする(-pix_fmt yuv420pがミソだった)。
ffmpeg -loop 1 -i img.jpg -i snd.m4a -ab 24k -vb 72k -c:v libx264 -pix_fmt yuv420p -shortest out.mp4
また,2つのmp4ファイルを結合するには次のようにする。
ffmpeg -safe 0 -f concat -i mylist.txt -c copy out3.mp4
ただし,mylist.txtには結合前のファイルを並べておけば良い。
cat mylist.txt (out?.mp4は同じコーデックで作ったファイルであること)
file ./out1.mp4
file ./out2.mp4
あとはコンテンツだ。熊本大学の鈴木克明さん(昔,日本文教出版の高等学校の情報の洋教科書でいろいろお世話になった。今,日本教育工学会の会長になっておられた)が上のシンポジウムで指摘していたように,無理せずにゆるゆると真の目的を見据えながらやるのがよろしいようだ。
遠隔授業のばたばた(3)に続く
2020年4月17日金曜日
米国の集団免疫率(2)
米国の集団免疫率(1)からの続き
トランプは4/17の会見で米国におけるCOVID-19の死亡数は6〜6.6万人にとどまるとした。これは勝手な想像ではなく,IHMEの最新の予測である。前回の10〜25万人から減少させたことを自分の政策の成果であるかのようにアピールしつつ,ロックダウンを解消して経済回復を誘導しようという意図に基づくものだろう。
前回のSIIDR2モデルの適用はちょうど2週間前だったので,あらためてこのモデルと上記の主張を組み合わることで米国の集団免疫率を推定してみる。前回のように1ppm到達の基準日3/10から4/17までの39日分の新規感染数累計と死亡数累計の人口比データを示す。
- - - - - - - - - - - - - - - - - - - - - - - - - - - - -
xa=[0,1,2,3,4,5,6,7,8,9,10,11,12,13,
14,15,16,17,18,19,20,21,22,23,24,25,26,27,
28,29,30,31,32,33,34,35,36,37,38]
ya=[0.014,0.021,0.030,0.038,0.051,0.051,0.051,
0.106,0.107,0.215,0.317,0.462,0.462,0.958,
1.280,1.576,1.929,2.074,2.587,3.136,3.722,
4.268,4.953,5.684,6.483,7.335,8.310,9.327,
10.13,11.03,11.99,12.93,14.00,14.96,15.92,
16.81,17.55,18.33,19.20]
za=[0.06,0.08,0.09,0.11,0.12,0.12,0.12,
0.18,0.18,0.30,0.46,0.61,0.61,1.22,
1.43,2.04,2.68,3.01,3.77,5.06,6.41,
7.28,8.65,11.7,14.6,17.8,21.3,25.4,
29.0,32.9,38.7,44.5,50.4,56.2,62.0,
66.7,71.2,78.5,85.6]/100
- - - - - - - - - - - - - - - - - - - - - - - - - - - - -
SIIDR2の計算において次のパラメタを用いると上記の米国のデータが再現できる。
$\beta = 0.60, \nu =0.12, \lambda=28, \tau=16$, $\alpha_1=5/0.80, \alpha_2 = 5/0.20$, $\gamma_1 = 15/0.95, \gamma_2 = 15/0.06$。前回と異なり,$\gamma_2$の値は,中国や韓国などを説明した値の方にややに戻している。
トランプは4/17の会見で米国におけるCOVID-19の死亡数は6〜6.6万人にとどまるとした。これは勝手な想像ではなく,IHMEの最新の予測である。前回の10〜25万人から減少させたことを自分の政策の成果であるかのようにアピールしつつ,ロックダウンを解消して経済回復を誘導しようという意図に基づくものだろう。
前回のSIIDR2モデルの適用はちょうど2週間前だったので,あらためてこのモデルと上記の主張を組み合わることで米国の集団免疫率を推定してみる。前回のように1ppm到達の基準日3/10から4/17までの39日分の新規感染数累計と死亡数累計の人口比データを示す。
- - - - - - - - - - - - - - - - - - - - - - - - - - - - -
xa=[0,1,2,3,4,5,6,7,8,9,10,11,12,13,
14,15,16,17,18,19,20,21,22,23,24,25,26,27,
28,29,30,31,32,33,34,35,36,37,38]
ya=[0.014,0.021,0.030,0.038,0.051,0.051,0.051,
0.106,0.107,0.215,0.317,0.462,0.462,0.958,
1.280,1.576,1.929,2.074,2.587,3.136,3.722,
4.268,4.953,5.684,6.483,7.335,8.310,9.327,
10.13,11.03,11.99,12.93,14.00,14.96,15.92,
16.81,17.55,18.33,19.20]
za=[0.06,0.08,0.09,0.11,0.12,0.12,0.12,
0.18,0.18,0.30,0.46,0.61,0.61,1.22,
1.43,2.04,2.68,3.01,3.77,5.06,6.41,
7.28,8.65,11.7,14.6,17.8,21.3,25.4,
29.0,32.9,38.7,44.5,50.4,56.2,62.0,
66.7,71.2,78.5,85.6]/100
- - - - - - - - - - - - - - - - - - - - - - - - - - - - -
$\beta = 0.60, \nu =0.12, \lambda=28, \tau=16$, $\alpha_1=5/0.80, \alpha_2 = 5/0.20$, $\gamma_1 = 15/0.95, \gamma_2 = 15/0.06$。前回と異なり,$\gamma_2$の値は,中国や韓国などを説明した値の方にややに戻している。
2020年4月16日木曜日
遠隔授業のばたばた(1)
今,日本中の大学教員が試行錯誤の真っただ中にいるはずだ。Facebookの「新型コロナ休講で,大学教員は何をすべきかについて知恵と情報を共有するグループ」には今日現在で15,000人以上が登録している。令和元年度の学校基本調査では,大学教員の数は19万人弱なので,その8%程度に相当する。なかなか壮観だ。
私も,大阪教育大学で使われてきたmoodleの利用支援の猫の手として活動をすることになった。4月20日からインターネットを活用した授業がはじまるので待ったなしだ。通常の対面授業は5月11日(月)から再開する予定だが,今後の感染拡大の状況によっては,感染拡大防止期間を延長し,引き続きインターネットを活用した授業等を行うということなのでますます大変である。通年で3800科目あるうち前期が半分だとして1900科目,そのうち1100科目のコースがmoodle上に観測された。約6割に相当する。実験・実習・演習科目などもたくさんあるので,これらがどうなるのかは心配だ。
さて,自分が前期に担当する演習・実験以外の授業は3科目(古典力学・科学のための数学・電磁気学)だ。moodleのコースの枠組みは3回分作成したが,問題はコンテンツである。とりあえず,ギガに優しい田崎晴明さん方式でやることを想定している。写真にとって pdf化したノートと,iPhoneもしくはiPadで録音した音声データは,MicrosoftのOneDriveに置くことにする。なお,m4a音声データは,次のようにmp3に変換する予定である。
m4aからmp3への変換
・Apple Music App を開く
・メニューバーで「ミュージック」>「環境設定」の順に選択
・「ファイル」タブをクリックし、「読み込み設定」をクリック
・「読み込み方法」の横のメニューをクリックし、曲の変換先の
エンコード形式を選択,「OK」をクリック
・キーボードの「option」キーを押しながら「ファイル」>「変換」>
「[環境設定で指定した読み込み方法]に変換」の順に選択
・読み込んで変換したい曲が入っているフォルダまたはディスクを選択
変換前の形式の曲と、変換後の曲がライブラリに表示
それでもなお,板書形式が可能かどうかを模索している。
① Notabilityがよいということだったが,OneDriveに置こうとして撥ねられた。
② Goodnote5と画面記録がよいということで,画面記録アプリをさがしたところ,
DU-Recorder(App内課金が高額),ApowerREC(機能しませんでした)があった。
③ iPadとMacを有線で結んで,Mac側のQuickTimeで録画先をiPadに指定して録画する
方法があった。これはうまくいった。ただ,45分で200MBを越えるのでどうするか。
④ この場合でも,NotabilityよりはGoodnote5のほうがなんとなく使いやすそうである。
⑤ PC側のzoomの録画の方が便利ではないか,ということで,上記の設定をzoom側で
保存してみたところ,終了時に録画ファイルをm4aに変換してくれた。まあまあ。
試行錯誤は続く・・・というかもうあまり時間が残されていない。
遠隔授業のばたばた(2)に続く
私も,大阪教育大学で使われてきたmoodleの利用支援の猫の手として活動をすることになった。4月20日からインターネットを活用した授業がはじまるので待ったなしだ。通常の対面授業は5月11日(月)から再開する予定だが,今後の感染拡大の状況によっては,感染拡大防止期間を延長し,引き続きインターネットを活用した授業等を行うということなのでますます大変である。通年で3800科目あるうち前期が半分だとして1900科目,そのうち1100科目のコースがmoodle上に観測された。約6割に相当する。実験・実習・演習科目などもたくさんあるので,これらがどうなるのかは心配だ。
さて,自分が前期に担当する演習・実験以外の授業は3科目(古典力学・科学のための数学・電磁気学)だ。moodleのコースの枠組みは3回分作成したが,問題はコンテンツである。とりあえず,ギガに優しい田崎晴明さん方式でやることを想定している。写真にとって pdf化したノートと,iPhoneもしくはiPadで録音した音声データは,MicrosoftのOneDriveに置くことにする。なお,m4a音声データは,次のようにmp3に変換する予定である。
m4aからmp3への変換
・Apple Music App を開く
・メニューバーで「ミュージック」>「環境設定」の順に選択
・「ファイル」タブをクリックし、「読み込み設定」をクリック
・「読み込み方法」の横のメニューをクリックし、曲の変換先の
エンコード形式を選択,「OK」をクリック
・キーボードの「option」キーを押しながら「ファイル」>「変換」>
「[環境設定で指定した読み込み方法]に変換」の順に選択
・読み込んで変換したい曲が入っているフォルダまたはディスクを選択
変換前の形式の曲と、変換後の曲がライブラリに表示
① Notabilityがよいということだったが,OneDriveに置こうとして撥ねられた。
② Goodnote5と画面記録がよいということで,画面記録アプリをさがしたところ,
DU-Recorder(App内課金が高額),ApowerREC(機能しませんでした)があった。
③ iPadとMacを有線で結んで,Mac側のQuickTimeで録画先をiPadに指定して録画する
方法があった。これはうまくいった。ただ,45分で200MBを越えるのでどうするか。
④ この場合でも,NotabilityよりはGoodnote5のほうがなんとなく使いやすそうである。
⑤ PC側のzoomの録画の方が便利ではないか,ということで,上記の設定をzoom側で
保存してみたところ,終了時に録画ファイルをm4aに変換してくれた。まあまあ。
試行錯誤は続く・・・というかもうあまり時間が残されていない。
遠隔授業のばたばた(2)に続く
2020年4月15日水曜日
モビリティデータ
Appleが,新型コロナウイルス感染症(COVID-19)拡大防止に向けた世界各地での活動を支援するため,Appleマップによるモビリティデータの傾向を示すデータ(Apple Maps Mobility Trends Reports)を提供した。
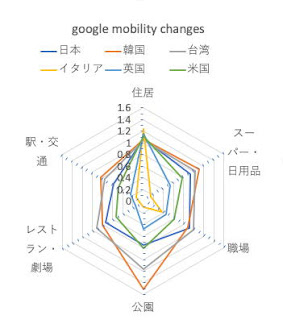
しばらく前にはgoogleも同様のデータ(COVID-19 Community Mobility Reports)を公開していた。例えば日本の時系列はpdfファイルとして提供されている。このデータを再構成して,4月5日の時点でのいくつかの国の特徴を比較したものが次の図である。
アップルの方は,上方の種類は限定されているが,時系列のCSVデータも提供されていてありがたい。ここではその結果だけを例示してみよう。
しばらく前にはgoogleも同様のデータ(COVID-19 Community Mobility Reports)を公開していた。例えば日本の時系列はpdfファイルとして提供されている。このデータを再構成して,4月5日の時点でのいくつかの国の特徴を比較したものが次の図である。
図1 グーグルモビリティトレンドからの4/5の傾向(平常時との比率)
アップルの方は,上方の種類は限定されているが,時系列のCSVデータも提供されていてありがたい。ここではその結果だけを例示してみよう。
図2 日本のモビリティトレンド(1/13-4/15)
図3 韓国のモビリティトレンド(1/13-4/15)
日本の3月下旬の緩みがはっきりと現れている。まだまだ活動制限のレベルは不十分であり,西浦博さんがあせって,重篤者85万人,死者40万人という発表を(遅すぎると思うが)したのもわからなくはない。しかし前提条件がよく理解できないのだ。例えばNHKのニュースでは,以下のような説明があったが・・・
外出自粛などの感染防止対策を何も行わなかった場合、感染が広がり始めてからおよそ60日でピークを迎えると推計しています。
その場合の重篤な患者は合計で▽15歳から64歳まででおよそ20万人、▽65歳以上で65万人の合わせておよそ85万人に上るとしています。
その場合、人工呼吸器が足りず、必要な治療が受けられなくなり、中国でも重篤患者の半数が死亡しているという研究があるということで、日本国内でも半数にあたるおよそ40万人以上が死亡すると推計しています。
いずれにせよ,相変わらず安倍政権支持率は40%の水準を維持しており,日本の政治はびくともしていない。
2020年4月14日火曜日
基準の変更と比較
アジアの状況,欧州の状況,からの続き
アジア太平洋と欧州・北米の新規感染者数累計を人口で規格化したグラフを考えてきた。これを並べて比較してみる。これまでは基準を人口の1ppmを越えた時点としてこれを各国の共通の原点とした対数グラフを考えた。その基準点を人口の10ppmになった時点に変更して比べてみる。累計数がかなり増加してきたため,最近の特徴をよく観察したいと思ったので。
アジア太平洋と欧州・北米の新規感染者数累計を人口で規格化したグラフを考えてきた。これを並べて比較してみる。これまでは基準を人口の1ppmを越えた時点としてこれを各国の共通の原点とした対数グラフを考えた。その基準点を人口の10ppmになった時点に変更して比べてみる。累計数がかなり増加してきたため,最近の特徴をよく観察したいと思ったので。
図1 アジア・太平洋地域の新規感染数累計対人口比の推移(100ppm)
図2 欧州・北米地域の新規感染数累計対人口比の推移(100ppm)
イランは比較のために両方のグラフに含めている。欧米はすべてイランを上回っている。グラフで示した欧米主要国の新規感染数累計は人口比ではすでに湖北省を越えているわけだ。しかし,アジアでは震源地の中国湖北省以外はすべてイランの水準を下回っている。
①欧米は同じ傾向で推移している。指数関数的増加の時定数がしだいに減りつつある
②アジアは,中国が既に収束し,韓国がこれに続いている。
③オーストラリア,香港,マレーシアも減速の兆が見える。
④台湾は一貫して低水準に押さえ込んでいる。
⑤シンガポールは当初,台湾や香港と並んだ優等生だったが,その後抑え切れていない。
⑥日本(東京)は,ほぼ一定の時定数での指数関数的な増加を続けている(新規感染数累計は1.107倍/日,死亡数累計は1.046/日の割合で増えている)。
もし,この定数が変化しなければ,緊急事態宣言の期限である5月6日には日本の新規感染数累計は6万人に達する。これは人口比で500ppmであり,韓国の200ppmや湖北省(武漢以外)の370ppmを超える水準に相当する。また,このときの死亡数は260人程度にとどまり,そのまま推移すれば,死亡数(5/6の21日後)/新規感染数累計(5/6) = 1%というリーズナブルな値が得られる(感染数と死亡数の間に21日程度の遅れがあると仮定している)。
2020年4月13日月曜日
2020年4月12日日曜日
アジアの状況
新型コロナウイルス感染症の感染者数の増加が5/6には収まるように考えている人が多いのかもしれない。うまくいけば7月には一端終息に向ったようにみえる可能性もある。しかし,集団免疫が獲得できずワクチンもない現状では,緊急事態宣言レベルの制限を継続するか,断続的に緩めたり強めたりすることの繰り替えしかの二択ではないだろうか。中国以外で終息に近い状態を実現しているのは台湾だけだ。それに近いのは韓国。香港もシンガポールも完全にはおさまっていない。どこまで耐えられることか。
図1 人口当りの新規感染数累計(単位100ppm,基準日は1ppm達成時)
図2 人口当りの新規感染数累計の対数(100 ppm,基準日は1ppm達成時)
注:上記は武漢を除いた湖北省の値であり,370ppmに収束している。武漢を含めた湖北省の収束値は1150ppmであり,上記の3.1倍に相当する。湖北省の全体イメージは湖北省(武漢以外)を全体に3倍程度スケールしたものと考えられることに注意する。
2020年4月11日土曜日
2020年4月10日金曜日
BCG
Wikipediaによれば,BCG とは次のようなものだった。
自分が小学生低学年の間は陰性が続いていて,ほぼ毎年のようにBCGを注射していたような気がする。1回くらいのBCGでは抗体ができなかったということか。で,BCGも初めのうちは今のようなスタンプ型ではなかった。それがいつの間にか(日本では1974年から)定期化され全員接種に切り替わっていた。
そのBCGが新型コロナウイルス感染症に効果があるかどうかということで議論になっている。乳児向けのBCGが不足することがないように祈るだけである。
BCGは,実験室で長期間培養を繰り返すうちにヒトに対する毒性が失われて抗原性だけが残った結核菌であり,BCGワクチンはBCGを人為的にヒトに接種して感染させることで,結核に罹患することなく結核菌に対する免疫を獲得させることを目的としたものである。小学生の時には,毎年ツベルクリン反応を調べる注射が恒例行事だった。ツベルクリン(独: Tuberkulin)とは,結核菌感染の診断に用いられる抗源である。前腕の内側に注射して数日後にこれが赤く腫れている(陽性)か変化なし(陰性)かを透明の物差しで測って確認する。たぶん1cm以上のサイズなら陽性なのでこれでOKだ。それ未満なら陰性や疑陽性,すなわち結核菌に対する抗体がないので,BCGを注射しなければならない。したがって小学生にとってはこれはなかなかドキドキする検査なのである。
自分が小学生低学年の間は陰性が続いていて,ほぼ毎年のようにBCGを注射していたような気がする。1回くらいのBCGでは抗体ができなかったということか。で,BCGも初めのうちは今のようなスタンプ型ではなかった。それがいつの間にか(日本では1974年から)定期化され全員接種に切り替わっていた。
そのBCGが新型コロナウイルス感染症に効果があるかどうかということで議論になっている。乳児向けのBCGが不足することがないように祈るだけである。
2020年4月9日木曜日
緊急事態宣言と接触制限モデル(3)
緊急事態宣言と接触制限モデル(2)からの続き
4月7日のtwitterで牧野淳一郎さんがいうには,
上に示されている数字は行動抑制の因子であり,モデルの感染率にかける係数だと思われる。ここでは,どれが正しいかについては考察せずに,ドイツなど欧州の基本再生産数$R_0=2.5$(7日増倍率が7倍)に基づいた西浦さんの計算(我々の評価では$R_0=2.3$だったが)を,東京の現状に合わせて再計算した結果を報告する。
前回述べたように,現在の東京では,7日増倍率が2.5倍($R_0=1.65$)程度なので,西浦さんが用いている値よりかなり小さいのだ。単純なSIRモデルを用いてこれを再現するパラメタセットを探し,その場合に接触制限の効果がどうなるかを調べよう。
やり方は前回と同じなので,パラメタを示す。β=0.28,初期値はν=0.005とすれば上記の増倍率が再現できた。つまり,さきのMathematicaコードにおいて,
- - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
f[n_, β_, α_, ν_, p_]:=
NDSolve[{S'[t]==-(p+(10-p)*Tanh[2*(20-t)])/10*β/n*J[t]*S[t],
J'[t]==(p+(10-p)*Tanh[2*(20-t)])/10*β/n*J[t]*S[t]-J[t]/α,
R'[t]==J[t]/α, S[0]==n, J[0]==ν, R[0]==0}, {S,J,R}, {t,0,100}];
n=1400; β=0.28; ν=0.005; p=10;
sol = f[1400, β, 7, 0.005, p];
s[t_] := S[t] /. sol[[1, 1]];
i[t_] := J[t] /. sol[[1, 2]];
cft1[t_]:= (p+(10-p)*Tanh[2*(20-t)])/10*β/n*i[t]*s[t];
・・・
Plot[{cf1[t], cf2[t], cf3[t], cf4[t], cf5[t], cf6[t]},
{t, 10, 30}, PlotRange -> {0, 0.1},
GridLines -> {{19, 20, 21}, {0.005, 0.01, 0.015, 0.02, 0.025}}]
- - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
などとすると計算結果は次のようになった。
4月7日のtwitterで牧野淳一郎さんがいうには,
一応どれも現実をモデルしているはずのところで、そこまで行動抑制しないといけない割合が、西浦氏:0.2、大橋氏「0.45](R_0>1でいくとして)、佐藤氏 0.02 で3人で20倍違う時点で少なくとも2人は間違っているのは明らかであろう。西浦氏は,緊急事態宣言と接触制限モデル(1)で取り上げた西浦博さん(北海道大学),大橋氏は,新型コロナウイルス感染症の 流行予測の大橋順さん(東京大学),佐藤氏は,COVID-19情報共有の佐藤彰洋さん(横浜国立大学)である。
上に示されている数字は行動抑制の因子であり,モデルの感染率にかける係数だと思われる。ここでは,どれが正しいかについては考察せずに,ドイツなど欧州の基本再生産数$R_0=2.5$(7日増倍率が7倍)に基づいた西浦さんの計算(我々の評価では$R_0=2.3$だったが)を,東京の現状に合わせて再計算した結果を報告する。
前回述べたように,現在の東京では,7日増倍率が2.5倍($R_0=1.65$)程度なので,西浦さんが用いている値よりかなり小さいのだ。単純なSIRモデルを用いてこれを再現するパラメタセットを探し,その場合に接触制限の効果がどうなるかを調べよう。
やり方は前回と同じなので,パラメタを示す。β=0.28,初期値はν=0.005とすれば上記の増倍率が再現できた。つまり,さきのMathematicaコードにおいて,
- - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
f[n_, β_, α_, ν_, p_]:=
NDSolve[{S'[t]==-(p+(10-p)*Tanh[2*(20-t)])/10*β/n*J[t]*S[t],
J'[t]==(p+(10-p)*Tanh[2*(20-t)])/10*β/n*J[t]*S[t]-J[t]/α,
R'[t]==J[t]/α, S[0]==n, J[0]==ν, R[0]==0}, {S,J,R}, {t,0,100}];
n=1400; β=0.28; ν=0.005; p=10;
sol = f[1400, β, 7, 0.005, p];
s[t_] := S[t] /. sol[[1, 1]];
i[t_] := J[t] /. sol[[1, 2]];
cft1[t_]:= (p+(10-p)*Tanh[2*(20-t)])/10*β/n*i[t]*s[t];
・・・
Plot[{cf1[t], cf2[t], cf3[t], cf4[t], cf5[t], cf6[t]},
{t, 10, 30}, PlotRange -> {0, 0.1},
GridLines -> {{19, 20, 21}, {0.005, 0.01, 0.015, 0.02, 0.025}}]
- - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
などとすると計算結果は次のようになった。
図 SIRモデル+シグモイド関数制限措置による新規感染者数の変化(東京のデータ)
(上から順に,青:制限なし,80%,60%,50%,40%,20%に制限)
増加と減少の臨界点は50%あたりにある。すなわち,数字だけでいえば大橋氏の値と近い結果が得られたのかな。大橋氏の資料に対する牧野さんのもろもろの批判にはうなずけるものもあるけれど。そう,このブログも拡散してはいけない情報の仲間である。
まとめ
新型コロナウイルス感染症専門家会議(というか西浦博さん)から出てきた接触8割削減の前提条件は,欧州並の$R_0=2.5$に対応する場合ということだった。それを現在の東京の$R_0=1.65$に対応させると,上記のように接触6割削減で新規感染数は減少させることができる。いずれにせよモデル計算の結果なので,他地域の今後の動向や安全率も勘案して,目標値として接触8割削減を掲げることは意味があるだろう。
P. S. 佐藤彰洋さんのシミュレーションに対する疑義がでてきた。ちょっと安心した。Delay Differential Equationによるモデリングは,それでもまだ自分には理解できていない。
P. P. S. 4/10に牧野淳一郎さんの解説が出てきたので問題点がよく理解できるようになった。ただ,6割削減でも新規感染数が減少に転ずるという牧野さんの解説は,7割削減が必要であるというこちらの結果とは食い違っていた。
[1]人との接触7~8割減、効果は 専門家「感染抑制できる」、全員やれば6割減でも 新型コロナ(朝日新聞)→タイトルと本文があまり整合していない記事
[2]佐藤彰洋氏(横浜市大)の新型コロナ感染予測シミュレーションに関する疑義について(本堂毅・佐野雅己・松下貢)
[3]いろいろなモデル計算(牧野淳一郎,2020.4.10)
[4]交通整理(牧野淳一郎,2020.4.12)
[5]公開質問状に対するコメント(佐藤彰洋,2020.4.13)
[6]交通整理の続き(牧野淳一郎,2020.4.12)
[7]交通整理の続きその2(牧野淳一郎,2020.4.16)
[8]新型コロナウイルス感染症対策専門家会議の見解等(牧野淳一郎,2020.4.18)
2020年4月8日水曜日
緊急事態宣言と接触制限モデル(2)
緊急事態宣言と接触制限モデル(1)からの続き
緊急事態宣言がでた翌朝(4/8)の日本経済新聞にも再び西浦さんの図が「感染拡大阻止 接触8割減が必要」という記事とともに掲載されていた。安倍晋三も同内容を専門家の見解として強調していた。
緊急事態宣言がでた翌朝(4/8)の日本経済新聞にも再び西浦さんの図が「感染拡大阻止 接触8割減が必要」という記事とともに掲載されていた。安倍晋三も同内容を専門家の見解として強調していた。
図 日本経済新聞(2020.4.8 朝刊3面)から引用
日経の記事を批判的に読み解いてみる。
①「接触8割減」は政府の専門家会議メンバーで,感染者数の予測を数理モデルで解析している北海道大学の西浦博教授がはじいた数字だ 。
→ 西村さんは新型コロナウイルス感染症対策専門家会議の当初の構成員ではなかった。クラスター対策班のメンバーか。
②1人の感染者が平均で何人に感染させたかを示す「実効再生産数」は3月21〜30日の改定データで推定1.7。
→新規感染者数累計の1週間の増倍率を$k$とすると,実効再生産数$R_0$との間に,$R_0=1+5/7*\log k $の関係がある(倍加時間と基本再生産数)。東京(3/20-3/31)のデータは,平均で$k=2.3$であることから,$R_0=1.6$となった(注:$R_0=1.7$に対応するのは$k=2.7$)。
③その時点では数万人の感染者が出ていたドイツ(2.5)を下回っていたが,
→ドイツ(3/20-3/31)のデータは,平均で$k=3.9$であることから,$R_0=2.0$となった(注:$R_0=2.5$に対応するのは$k=8$,3/10以前には$k=8$を超えていたが・・・)。
④4月に入っても感染増が続き,実効再生産数は3を超えてドイツを上回った可能性があるという。
→実効再生産数がを3を超えるとは。$R_0=3$に対応するのは$k=16$である。日本でそのようなタイミングがあったのだろうか。福岡で9倍,福井で20倍くらいのタイミングは一時的に見られるが,これらはいずれも感染数が少なくて揺らぎが効いてしまう段階の話である。
⑤このままだと1日あたりの新規感染が米ニューヨークのように数千人に達する。
→仮定が④であれば正しいし,指数関数的な増大であれば常に正しい言明ではあるが,事態を強調するためにやや話を盛っている印象を受けた。
ただし,新規感染数累計について単純な指数関数型増加傾向が続くと仮定すると(接触制限の効果がない場合),直近の増倍率は東京で1.15/日,大阪で1.10/日となっているので,
東京:4/14:3千人,4/21:8千人,4/28:2万人,5/5:5万人
大阪:4/14:1千人,4/21:2千人,4/28:4千人,5/5:8千人
である。1日あたりの数ではなく累計であることに注意。
図 新規感染数の1週間増倍率$k$と実効再生産数$R_0$
登録:
コメント (Atom)