３７．서울 행 비행기 표를 예약하고 싶어요.
Soeul haeng bihaenggi pyoreul yeyakago sipeoyo.
ソウル行きの飛行機のチケットを予約したいです。
2025年7月31日木曜日
2025年7月29日火曜日
2025年7月28日月曜日
2025年7月27日日曜日
2025年7月26日土曜日
2025年7月25日金曜日
2025年7月24日木曜日
パデ近似（３）
パデ近似（２）からの続き
では，$\log x$ の近似式はどうして導かれたのか。ChatGPT o3に教えてもらうことにした。
(1) $x=t^2$ とおいて，$f(x) = \log x = 2 \log t = g(t)$
(2) $h=t-1$ とおいて，$t=1 \ (x=1)$のまわりでパデ近似を行う。
(3) テイラー展開すると， $g(t) = 2 \log(1+h) = 2 (h - \frac{1}{2} h^2 + \frac{1}{3} h^3 -\frac{1}{4} h^4 + \cdots)$
(4) これを $h$について パデ近似して$P_{2,2}(h)$ を求めると$P_{2,2}(h) = \dfrac{2h+h^2}{1+h+\frac{1}{6} h^2}$
(5) これを $h=t-1$ で $t$の関数に戻すと，$g(t) \approx \dfrac{6(t^2-1)}{1+4t+t^2}$ となる。
(6) さらに $t=\sqrt{x}$ で $x$の関数に戻すと，$f(x) \approx \dfrac{6(x-1)}{1+4 \sqrt{x} + x}$となる。
こうして$\log x \approx \dfrac{6(x-1)}{1+4 \sqrt{x} + x}$ が得られた。なるほどね。
じゃあ，次数を上げて計算し，自分が本当に理解したかどうかチェックしてみよう。
(7) $g(t) = 2 \log(1+h) = 2 (h - \frac{1}{2} h^2 + \frac{1}{3} h^3 -\frac{1}{4} h^4 + \frac{1}{5} h^5 -\frac{1}{6} h^6 + \cdots)$
(8) $P_{3,3}(h) = \dfrac{2h+2h^2+\frac{11}{30}h^3}{1+\frac{3}{2}h+\frac{3}{5}h^2+\frac{1}{20}h^3}$
(9) $g(t) \approx \dfrac{2 (-11 - 27 t + 27 t^2 + 11 t^3)}{3 (1 + 9 t + 9 t^2 + t^3)}$
(10) $f(x) \approx \dfrac{2 (-11 - 27 \sqrt{x} + 27 x + 11 x \sqrt{x}}{3 (1 + 9 \sqrt{x} + 9 x + x \sqrt{x})}$
グラフをみるといちおうもっともらしい。
図：$\sqrt{x}$を含んだパデ近似
実はMathematicaにはパデ近似を求める関数があるので，原点以外でも簡単に求まる。
PadeApproximant[2(t-1)-(t-1)^2+(2(t-1)^3)/3-(t-1)^4/2, {t, 1, {2, 2}}]
まあ，さきほどのチェックでも連立方程式を解いてもとの変数に戻すところはMathematicaの力を借りている。3元連立方程式を間違えずに解くのは筋トレ以上にたいへんだ。そういえば，中学生のときは2元連立方程式がちょっと苦手だったかもしれない。
2025年7月23日水曜日
Jupyterつまづく
Jupyterからの続き
Mathematica ノートブックにインスパイアされて登場したJupyterは，自分のpythonやJuliaの実行環境になっている。とても便利だ。
ところが，homebrew で jupyterlab4.4.5に更新したところ，jupyter lab や jupyter notebook が動かなくなってしまった。困ったぞ。
いろいろ調べてみると，悪さをしているのはSafari のようだ。どうも最近「この接続は安全ではありません」というhttpsにかかわる警告が多いと感じていた。ChatGPT o3に聞いてみると，それが原因だった。
Ａ（ChatGPT o3）：
（前後略）Safari 18 以降（macOS Sonoma/iOS 18 ベータなど）には 「HTTP はブロックして常に HTTPS だけ許可」 という新機能があります。これが有効になっていると、たとえ localhost（127.0.0.1）でも http://… へのアクセスは遮断され、画像のようなエラーNavigation failed because the request was for an HTTP URL with HTTPS‑Only enabled (WebKitErrorDomain: 305)が表示されます。ローカル開発サーバや Jupyter Lab は既定で HTTP を使うため、Safari が弾いてしまうわけです。
解決方法も教えてくれたのだけれど，SSLの証明書を設定するところがどうもうまくいかない。困った。デフォルトのブラウザをSafari から Chrome にスイッチすると，Chrome では jupyter lab が起動したのでとりあえずはOKだが，それはそれで面倒な気もする。
四苦八苦してChatGPT o3を問いただした結果，次のようにすればよい。
Step 1 : Jupyter Lab を HTTP で起動ターミナルを開くつぎのコマンドを実行# 証明書オプションを付けずに純粋な HTTP で起動jupyter lab --port 8889 --ip 127.0.0.1 --no-browser起動ログにhttp://127.0.0.1:8889/lab?token=dfbc5bbd50a3b13f317435a1bfa1245684e3f0afd315ba96が表示されれば サーバは準備完了（緑色の [I ... ServerApp] 行が目印）。
このURLをブラウザに直接貼付けたところうまくいったので，これでよしとする。
2025年7月22日火曜日
第27回参議院議員通常選挙（２）
第27回参議院議員通常選挙（１）からの続き
3年前（2022年）の参議院選挙で，参政党は選挙区45名，比例区5名の計50名の候補者を出して，神谷宗幣の1議席を獲得した。その当時は，幸福実現党，ごぼうの党，日本第一党，新党くにもり，維新政党・新風，ファーストの会など10名-12名の候補者を立てた有象無象の諸派と同じグループの極右カルト政党だった。彼らには大量候補者を立てる資金力があったことだけが他党とは異なっていた（いまみるとごぼうの党の政策のほうがよほどましだ）。
今回の参政党は比例区に10名候補者を出して比例得票数で第3党になってしまった。神谷と併せ参議院議員が15名。選択的夫婦別姓はもう無理だとの声も。テレビには熱狂な支持者の群れと若年層の肯定的なコメントが溢れていた。まあ，政治的なブームというのはいつもこうなのかも知れない。極右健康カルトに若い女性候補者と微妙なシンタックスシュガーを混ぜてマルチ商法のテクニックを使っているため，従来型の典型的極右よりも取り扱いが面倒だ。
比例代表１．自由民主党 1281万票 21.6%２．国民民主党 762万票 12.9%３．参政党 743万票 12.5%４．立憲民主党 740万票 12.5%５．公明党 521万票 8.8%６．日本維新の会 438万票 7.4%７．れいわ新選組 388万票 6.6%８．日本保守党 298万票 5.0%９．日本共産党 286万票 4.8%10．チームみらい 152万票 2.6%11．社会民主党 122万票 2.1%12．NHK党 68万票 1.2%選挙区北海道：［自・立・自］＿参：田中義人53（12.8%）青 森：［立］＿自・参：加藤勉65（16.7%）岩 手：［立］＿自・参：及川泰輔46（18.5%）宮 城：［立］＿自・参：ローレンス綾子55（17.9%）秋 田：［無］＿自・参：佐藤美和子65（13.1%）山 形：［無］＿自・参：佐藤友昭52（12.5%）福 島：［自］＿立・参：大山里幸子51（21.5%）茨 城：［自］＿参・立：桜井祥子41（24.8%）栃 木：［自］＿立・参：大森紀明54（22.1%）群 馬：［自］＿参・立：青木ひとみ44（31.5%）埼 玉：［自・国・立・参］＿公：大津力53（13.6%）千 葉：［国・立・自］＿参：中谷めぐ43（14.3%）東 京：［自・参・国・公・国・共・立］＿維：さや43（9.6%）神奈川：［立・国・自・参］＿公：初鹿野裕樹48（12.7%）新 潟：［立］＿自・参：平井恵里子46（19.0%）長 野：［立］＿自・参：竹下博善42（18.4%）山 梨：［国］＿自・参：永田己貴55（17.1%）富 山：［国］＿自・参：田保智世59（12.5%）石 川：［自］＿国・参：牧野緑40（12.5%）福 井：［自］＿国・参：千田崇裕39（12.5%）岐 阜：［自］＿立・参：瀬尾英志40（23.4%）静 岡：［国］＿自・参：松下友樹41（17.2%）愛 知：［国・立・参・自］＿公：杉本純子47（14.9%）三 重：［立］＿自・参：難波聖子45（24.2%）滋 賀：［自］＿国・維・参：中田あい46（17.8%）✓京 都：［維・自］＿共・参：谷口青人46（12.0%）大 阪：［維・維・参・公］＿自：宮出千慧40（12.1%）兵 庫：［無・公・自］＿維・参：藤原誠也37（10.3%）奈 良：［自］＿国・維・参：黒川洋司53（13.5%）✓和歌山：［無］＿自・参：林元政子51（19.8%）鳥取島根：［自］＿国・参：倉井克幸42（15.4%）岡 山：［自］＿立・参：広森志穂34（24.0%）広 島：［自・立］＿参：小石美千代56（21.3%）山 口：［自］＿参・国：山崎珠江47（22.5%）徳島高知：［無］＿自・参：金城幹泰43（20.4%）香 川：［国］＿自・参：小林直美51（14.5%）愛 媛：［無］＿自・参：原田慎太郎35（20.4%）福 岡：［自・参・公］＿国・立：中田優子35（16.6%）佐 賀：［自］＿立・参：下吹越優也32（18.5%）長 崎：［自］＿国・参：黒石隆太33（16.9%）熊 本：［自］＿立・参：山口誠太郎36（24.6%）大 分：［立］＿自・参：野中しんすけ38（20.1%）宮 崎：［立］＿自・参：滋井邦晃43（20.0%）鹿児島：［無］＿自・参：牧野俊一39（23.8%）沖 縄：［無］＿自・参：和田知久65（19.5%）
驚くことに参政党は選挙区で6名も当選している。選挙区の当選者+1-2のリストの内訳は，自(47)，参(45)，立(24)，国(18)，公(7)，維(7)，その他だ。当選者+1-2の範囲から参政党がはみ出た例外は滋賀県と奈良県だけ。図にあるような若年層の動向をみれば，これがそう簡単な一時的ブームといえるのかどうか。
図：かなりショックな年代別の比例投票先（NHKから引用）
［１］参政党は自民党の票を奪っているのか？（菅原琢）
［２］参政党は「第三極票」に乗った？（菅原琢）
［３］参政党のこれまでを振り返る(結党前史編)（雨宮純）
［４］それでも参政党を選びますか（Tansa）
2025年7月21日月曜日
第27回参議院議員通常選挙（１）
最近は期日前投票に行くことが多かったけれど，よく考えると特に用事がなければ地元の投票所でいいわけだ。ということで，7月20日朝7時頃を目指して自転車で小学校に向かう。
以前は，もう少し近くの自治会館が会場だった。それがよくわからない理由でいつの間にか校区の小学校に変更された。そのため投票所の面積が体育館くらいの広さから，小学校の玄関脇にある普通教室の半分くらいの面積の小部屋になってしまった。何だか狭いことこの上ないけれど，人口6万人に31投票所があるので，平均1800人の有権者，つまり毎分平均2.5人を捌けばいいので，こんなものかもしれない。
さて，朝6時55分に小学校の玄関につくと，すでにお爺さんが一人待っているので，自分は2番目のお爺さんだ，そうこうしているうちに後に3人の老人が続いた。ここで，時間になって玄関が開場された。一番目の人は投票箱の確認業務があるので（自分もむかし自治会館の投票所でやったことがある），ちょっと待ってくださいと，中が見渡せる投票部屋の入口で一時停止していた。
係の人は入口前整理1名，選挙区担当2名，比例区担当2名，投票立ち会い人2名くらいだった。投票済み証明書はどこにも，気配もなかった。帰りに入口の注意事項が目に入った。許可のないスマートフォンの使用はダメですというようなことが書いてある。まあそうだろう。
今回の選挙で気分が勝れないのは，参政党と国民民主党がずいぶん伸びそうなこと。なおかつ日本保守党やチームみらいまでおこぼれの議席を獲得しそうなこと。自民党および高齢化を続ける公明党と共産党は沈んでいく。若者の投票率は高そうだ。比例では若者の2割が国民，2割が参政を支持している。これが民主主義だというならばそうなのだろう。外山恒一は正しかった。
図：ChatGPT 4o が考えているちょっと微妙な投票所のイメージ
2025年7月20日日曜日
パデ近似（２）
パデ近似（１）からの続き
そんなわけで，$\displaystyle f(x) = \sum_{k=1}^\infty c_k x^{(k-1)/2}$として，同じようなことをすれば，$\sqrt{x}$を含んだ関数近似$f(x) = a(x)/b(x)$ ができるのではないかと考えた。
$f(x) = c_0 + c_1 \sqrt{x} + c_2 x + c_3 x\sqrt{x} + c_4 x^2+ c_5 x^2 \sqrt{x} + c_6 x^3 + \cdots$
$a(x) = a_0 + a_1 \sqrt{x} + a_2 x + a_3 x\sqrt{x} + a_4 x^2+ a_5 x^2 \sqrt{x} + a_6 x^3 + \cdots$
$b(x) = 1 + b_1 \sqrt{x} + b_2 x + b_3 x\sqrt{x} + b_4 x^2+ b_5 x^2 \sqrt{x} + b_6 x^3 + \cdots$
$a(x) = b(x) f(x) $ の両辺の係数を比較すると，
$x^0 \quad$： $a_0 = c_0$
$\sqrt{x}\ \ $： $a_1 = c_1 + c_0 b_1$
$x^1 \quad$： $a_2 = c_2 + c_1 b_1 + c_0 b_2$
$x^1 \sqrt{x}\ $： $a_3 = c_3 + c_2 b_1 + c_1 b_2 + c_0 b_3$
$x^2 \quad$： $a_4 = c_4 + c_3 b_1 + c_2 b_2 + c_1 b_3 + c_0 b_4$
$x^2 \sqrt{x}\ $： $a_5 = c_5 + c_4 b_1 + c_3 b_2 + c_2 b_3 +c_1 b_4 + c_0 b_5 $
$x^3 \quad$： $a_6 = c_6 + c_5 b_1 + c_4 b_2 + c_3 b_3 +c_2 b_4 + c_1 b_5 + c_0 b_6$
ここで，$f(x)=\log(1+x) = x -x^2/2 + x^3/3$として（$c_0=c_1=c_3=c_5=0$），
$a(x), b(x)$を$x\sqrt{x}$まで取ってみると，うまくかない。逆行列が作れず解なしになってしまう。しかたがないので，上の式を$c_8 x^4$まで拡張してようやく，$b_1=0, b_2=1, b_3=0, b_4=6$と，$a_0=0, a_1=0, a_2=1, a_3=0, a_4=1/2$が得られた。
なんのことはない，$\displaystyle f(x) = \dfrac{x+x^2/2}{1+x+x^2/6}$ で$\sqrt{x}$が含まれないものだった。チーン。
（注）これはChatGPTにも注意されたところだけれど，もとの問題 $\log(x)$ ではない。級数展開係数が簡単な $\log(1+x)$ で確認しようとしたものだ。$c_6 x^3$まででうまくいかなかったのは，（$c_k$にゼロが多くて）係数を決めるための条件が足りないからといわれた。
［１］Chemical reaction networks for computing logarithm（C. T. Chou）
［２］平方根を用いた立方根の近似と実装例（細田隆之）
2025年7月19日土曜日
パデ近似（１）
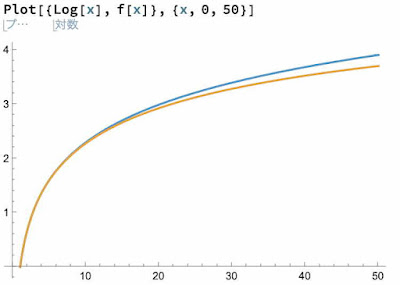
中嶋慧さんが，SNSで logの近似式についてリツイートしていた。log x = 6 (x-1)/(1+x+4√x) というものだ。見たことなかった。
図：Mathematicaで Log[x]とf[x_] := 6 (x - 1)/(x + 1 + 4 Sqrt[x]) を計算
その説明でパデ近似と関係があるようなニュアンスを見かけた。パデ近似はよく耳にしているけれどちゃんと勉強したことはない（あるいはきれいに忘れてしまったか）。
そこで，ちょっと調べてみた。
ある関数 $f(x) = c_0 + c_1 x + c_2 x^2 + \cdots + c_{m+n}x^{m+n}+ \cdots , c_k=\dfrac{f^{(k)}(0)}{k!}$ を 有理多項式$P_{m,n}(x) = \dfrac{a_0+a_1 x + a_2 x^2 + \cdots + a_m x^m}{1 + b_1 x + b_2 x^2 + \cdots + b_n x^n}$で近似するのがパデ近似だ。
$P_{m,n}(x)^{(k)}(0) = f^{(k)}(0), \quad (k=1,\cdots, m+n)$が成り立つように $P_{m,n}$ を定める。つまり，$f(x)$と$P_{m,n}(x) $が，$x=0$におけるテイラー展開の$m+n$次まで一致するということだ。係数全体を定数倍してもパデ近似は不変なので，$b_0=1$とする。
つまり，$c_k, \ \ (k=0,\cdots , m+n)$が与えられているときに，$a_i, \ (i=0, \cdots m)$ $b_j, \ (j=1, \cdots n) $ を求めるという問題だ。そこで，
$\dfrac{a_0+a_1 x + a_2 x^2 + \cdots + a_m x^m}{1 + b_1 x + b_2 x^2 + \cdots + b_n x^n} - (c_0 + c_1 x + c_2 x^2 + \cdots + c_{m+n}x^{m+n} ) = $
（$x$の$m+n+1$次以上の多項式X）
$a_0+a_1 x + a_2 x^2 + \cdots + a_m x^m =$
$ (1 + b_1 x + b_2 x^2 + \cdots + b_n x^n )( c_0 + c_1 x + c_2 x^2 + \cdots + c_{m+n}x^{m+n}) -$
（$x$の$m+n+1$次以上の多項式Y）
ここで，両辺について$x$の$m+n$次までの係数比較から，
$\displaystyle a_k = \sum_{i=0}^k c_i b_{k-i} \ (k = 0 , \cdots, m+n) $ ，ただし，$ a_j =0 \ (j>m), \ b_j = 0 \ (j > n) $
$a_j=0$となる式が $m+n-m=n$本あって，未知数の$b_j$が$n$個あるので，この連立方程式を解けば，$n$個の$b_j$ がすべて求まる。これを使って，$a_1 \cdots a_m$ が定まる。
2025年7月18日金曜日
Japan DashBoard
7月10日，内閣府とデジタル庁が「Japan Dashboard（経済・財政・人口と暮らしに関するダッシュボード）とデータカタログ」を公開した。
普通だと，ダッシュボードのトップページへのリンクがあって，そこにアクセスして話が進んでいくようなものだけれど，デジタル庁の該当ページは何だか面倒なことになっていた。
普通だと，ダッシュボードのトップページへのリンクがあって，そこにアクセスして話が進んでいくようなものだけれど，デジタル庁の該当ページは何だか面倒なことになっていた。
１．指標の分類この目次がいきなり登場するということは，ここがダッシュボードなのか？ここは単なるお知らせのページではなかったのか？わからない。あわててリンク先の内閣府のページに行くと内閣府側のまったく同じものに誘導された。わかりにくすぎる。とにかく，
２．Japan Dashboard
・指標のデータをみる
・1つの指標を都道府県ごとにみる
・2つの指標の関係性をみる
・4つの指標の推移を並べてみる
３．データカタログ
(1) 1つの指標のデータをコピーして利用する
(2) 複数の指標を一括ダウンロードする
４．関連資料
(1) Japan Dashboardの見方と操作方法
(2)「見える化」ポータルサイトのリニューアル方針
５．留意事項
691の指標を7つの大分類と62の中分類に分けて整理しています。人口：人口、婚姻・出生、高齢者割合等経済：県内総生産、就業・労働、所得・課税等教育：学校数・教員数、学校のICT環境等社会保障：医療体制、医療費、検診受診率等暮らし：安全、居住等社会基盤：社会基盤地方財政：基金、歳出・歳入等
について，都道府県別のデータ，2つの指標の相関と年次推移，4つの指標の比較などが上記の事例から選んで試せることだけがわかった。遊んでいるうちに思わぬ発見をするかもしれない。それにしても面倒だ。AI チャットボットに対話的に依頼するシステムにしてほしい。
図：Japan Dashboard で扱われるデータ項目一覧
2025年7月17日木曜日
オープンファクトリーマップ
1953年，日本でテレビ放送が始まった年に生まれたものだから，テレビが自分の情報源として身体に組み込まれてしまっている。困ったものだ。見るのはNHKとNHK Eテレと放送大学とBSの韓国ドラマが中心だ。報道番組ではBS-TBSの報道1930がかろうじて見ごたえがある。
NHKの夕刻のローカル番組ならナビで，奈良県のオープンファクトリーマップがとりあげられていた。オープンキャンパスの工場版？ちょっとちがうか。
［１］ 企業博物館（Wikipedia）
NHKの夕刻のローカル番組ならナビで，奈良県のオープンファクトリーマップがとりあげられていた。オープンキャンパスの工場版？ちょっとちがうか。
オープンファクトリーとは、簡単に言うと、工場を一般の人々に開放し、モノづくりの過程を見学したり、体験できるイベントのことです。従来は、個々の企業が自社の工場見学を実施することが一般的でしたが、近年では、地域全体の活性化を目指して、複数の企業が共同でイベントを開催する「地域一体型オープンファクトリー」が盛んになっています。これをマップアプリ上に展開したものがこれ。これがどんなシステム上で作られているかというと，プラチナマップというデジタルマッププラットフォームだった。事例紹介をみると，観光案内（金沢旅物語もあった）やMaaS（仙台MaaSとか）などが中心であり，奈良県のようなオープンファクトリーはちょっとめずらしいのかもしれない。近畿圏全域のオープンファクトリーマップのネットワークにして，初等中等教育に活用できるとおもしろそうだ。
図：奈良県オープンファクトリーマップのトップページ
［１］ 企業博物館（Wikipedia）
2025年7月16日水曜日
体温パリティ
身体の右側と左側で体温が違うって知っていましたか。
保育所でときどき発熱してママに連絡が行く風葉ちゃんだけれど，左38.0℃で右38.9℃だといわれたらしい。えっ体温は左右非対称なのか。熱力学はパリティ非保存ってことか。
ママの妹の看護師によれば，普通にあるあるの話らしい。自分は左腋窩でしか測らないので，左右非対称とか考えたこともなかった。口，肛門，耳内など場所によって違うということまではわかっていたけれど。
AIに聞いてみたら，もっともらしい説が返ってきた。身体の左側で測ったほうが高い場合が多いというデータがあるという。なぜならば，心臓の側の血流量が多いので左の体温が高いとかいうわけだ。ところが風葉ちゃんのいとこの紡木くんも，左37.6℃，右38.3℃で右側が高い。やはり当てにならないAIだ。
 |
図：体温パリティのイメージ（ChatGPT 4oによる） |
2025年7月15日火曜日
選択的夫婦別姓制度（２）
サザエさんからの続き
先日のNHKのニュースウォッチ９で，参院選がらみの選択的夫婦別姓制度が取上げられていた。前半は大阪・関西万博2025での外国人観光客へのインタビューで，各国夫婦の名前が違うとか，そもそも苗字がないとかいろいろだ。そういえば，昔ミャンマーからの留学生が研究室にいたが，彼女も苗字はないといっていた。夫婦別姓の中国人の賢い子供が，日本の同姓強要システムについてどう思うか問われ，それぞれの国の伝統や文化があるのだから，それに従えばよいと答えていた。
後半は，妻の意思を尊重して名前を変えるのが大変だった経営者の夫の話と，子供時代の自分の境遇から家族の名前の一体化がとても大事だという信念を持った女性の話で，男女それぞれから意見を聞きましたという構成になっていた。後者の論理は，子どもにとっては強制的だという藁人形論法と，私の知り合いで旧姓を使用してがんばって活躍できている人が沢山いますという友達います論法だった。そもそもNHKが世論調査項目を変えたことで，旧姓使用範囲拡大派の勢いを増してしまった。
芦田宏直の教育論はうなずけるところが多いのだけれど，その根拠となる家族論になるとどうなのだろうか。Facebookで次のように語っている。
「選択的夫婦別姓問題について。女性に不利という場合の不利は、制度をいじらなくても政策的にどうにでもなるので、大した問題ではないが、「〈家庭（家族）〉も個人の集まり」という意味での選択的夫婦別姓主張には、私は反対。〈家庭（家族）〉まで近代化してどうするというのだ。〈家庭（家族）〉というのは、もともと反社会的なものだ。〈家庭（家族）〉は、社会的な評価や〈契約〉によってまとまっている集団ではないのだから。」
まあ，制度がそのままでは政策的にどうにでもならないからこうなっているわけだけれど，自分も政治的なバイアスが強すぎて（それ自身は間違っていないのだが），家族とか名前の問題を本質的なレベルで十分に考えていなかったかもしれないと少しだけ反省した。
そこで，ChatGPT 4oのReseach に次のように聞いてみた。
Ｑ（koshix）：自分にとって，日本における氏（うじ），姓（かばね），本姓，姓（せい），名字，苗字などの定義や用法が混乱しています。そこで，この人の名前という重要な問題について歴史的な経緯と定義を時代を追って整理した上で，現代の法律的な表現と位置づけについて正しく定義して，できるだけわかりやすく理解できるように教えてください。なお，江戸時代以前で苗字がなかった人々に対する名前の命名方法なども含めて，すべての階層の人民についての議論をお願いします。できれば，社会経済学的な背景や，哲学的な裏付け，家族とは何かという本質論も踏まえていただければありがたいです。Ｑ（koshix）：1. 歴史的変遷と経済社会学的な意味と哲学的考察を中心にお願いします。 2. 歴史的変遷については古代から明治までの経緯を丁寧に追ってください。 3. 報告書スタイルでお願いします。
その結果得られたのが，日本人の氏名制度の歴史的編成だった。なかなかためになった。
もう一つはこれ。
Ｑ（koshix）：世界の各民族/各国で人の名前が姓＋名で構成されているのはなぜですか。姓の構成原理やあるいはミドルネームの意味は何ですか。哲学的・社会学的・経済学的な観点でその本質が何なのかを理論的・原則的に分析してください。
2025年7月14日月曜日
jReadability
量子コンピュータからの続き
日本語学習者向けのもので，日本語文章難易度判定システム（jReadability，難易度6段階判定），日本語学習者作文評価システム（jWriter，到達レベル5段階判定），日本語教育語彙集（JEV，18000語），機能後用例文データベース（はごろも）の４つのシステムから成り立っていて自由に使える。
早速，自分のブログテキストを日本語文章難易度判定システムに入れてみた。400字から1000字のテキストを受け付けるようになっている。「可視化機能を使用する」にチェックをいれると，ワードクラウド，語彙ネットワーク，意味階層図を出力してくれる。標準だと，テキスト情報，テキスト詳細，語彙リストが出てくる。
さて，「量子コンピュータ（13文，962字，229異形態素）」のリーダビリティは2.75であり，中級後半（ややむずかしい）となった。いいのか悪いのか。ひらがなが半分，和語が2/3で漢語が1/3，普通名詞が1/3で助詞助動詞が1/3。
図：ワードクラウドの結果
2025年7月13日日曜日
量子コンピュータ
量子超越性からの続き
量子コンピュータは日経新聞で時々話題の薪に火をくべられているが，話半分耳日曜で受け流している。そんな簡単に実用化レベルにはならないだろうと思っているからだ。
(1) Efficient Magic State Distillation by Zero-Level Distillation（T. Itogawa, Y. Takada, Y. Hirano, and K. Fujii）
量子コンピュータの最大のネックは準備した量子ビットが，環境との相互作用で量子回路による制御からはずれた状態に遷移して計算上のノイズになってしまうことだ。このため，1つの安定した論理量子ビットを構成するためにその数百倍を超える物理量子ビットが必要になってしまう場合もある。これが誤り耐性を持つ量子計算の問題である。
このためには普通「マジック状態」と呼ばれる特別な量子ビットを用意する必要があるが，そのための新しい方法を開発し，必要な計算機資源を従来より2桁減らすことができることを示した。これは量子コンピュータ実現への大きなステップだと考えられる。
(2) Cryptographic Characterization of Quantum Advantage（T. Morimae1, Y. Shirakawa, and T. Yamakawa）
量子コンピュータは，「古典コンピュータではすごく時間がかかるけどが量子コンピュータならすぐできる」ようなタスクを解ける=量子超越性を持つとされる。その例として量子コンピュータでは通常の計算機では手が出ない複雑な暗号が簡単に解けてしまうこと=暗号の安全性があげられた。しかしながら，これらの関係は必ずしも正確に定義されていたわけではなかった。
この論文では，量子計算の優位性という物理学と計算機科学にまたがる壮大なテーマに対し，一方向パズルというものを媒介として，ある種の暗号の安全性とある種の量子優越性の存在が必要十分条件で結ばれることを厳密に証明することに初めて成功した歴史的な業績と見なせる。
図：中性原子方式の量子コンピュータのイメージらしい（ChatGPT 4oから）
2025年7月12日土曜日
トランプからの手紙（３）
トランプからの手紙（２）からの続き
参考まで（ChatGPT 4o によればですけど，チョと怪しいけど，2023〜2024）
相互関税率の通知に係わる7月9日付のトランプからの手紙の第2弾が，Truth Socialで公開されていた。時間的な余裕はあったけれど，NHKの朝7時のニュースではまだ取上げられていなかった。誤表記や誤発音などの単純編集ミスは多いのに仕事が遅いNHK。
15 フィリピン 20%（17%）
16 ブルネイ 25%（24%）
17 モルドバ 25%（31%）
18 アルジェリア 30%（30%）
19 イラク 30%（39%）
20 リビア 30%（31%）
21 スリランカ 30%（44%）
22 ブラジル 50%（10%）
相変らず出鱈目のような気がする。ブラジルは，現在訴追中のボルソナーロ元大統領をトランプが支持しているため，アメリカの対ブラジル貿易は黒字なのにもかかわらず，内政干渉のために高額関税をかけることになった。もうなんでもありである。
トランプからの手紙は国名と関税率以外はすべて同じ文章なのだが，ブラジル宛のものは理由が別なので異なる文がついていた。
私は前大統領のジャイル・ボルソナロ氏と知り合い、取引をしたことがあり、彼を非常に尊敬していました。他の多くの国の指導者たちも同様でした。ブラジルが、在任中世界中で高く評価されていたボルソナロ前大統領を、アメリカ合衆国を含む各国から尊敬されていた人物として扱った方法は、国際的な恥辱です。この裁判は行われるべきではありません。これは即刻終了すべき魔女狩りです！ブラジルが自由な選挙に対する陰湿な攻撃を繰り返し、アメリカ人の基本的な言論の自由の権利を侵害していること（最近、ブラジル最高裁がアメリカ ソーシャルメディアプラットフォームに対し、数百万ドルの罰金やブラジル市場からの追放を脅迫する秘密かつ違法な検閲命令を数百件発行したことが示しています）、2025年8月1日から、ブラジルから米国に輸入されるすべてのブラジル製品に対し、セクター別関税とは別に50％の関税を課します。この50％の関税を回避するために転送される商品は、その高い関税の対象となります。DeepL.com（無料版）で翻訳しました。
図：これがブラジルです（ChatGPT 4o による）
Gemini 2.5 Flash DeepResearch調べによれば，2023年度において，
米国 輸出（2.3%） → 445億ドル → ブラジル 輸入（16% 第2位，中国 22%）
米国 輸入（1.2%） ← 390億ドル ← ブラジル 輸出（11% 第2位，中国 31%）
- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
米国の貿易黒字 55億ドル（≒8000億円）
米国 輸出（2.6%） → 797億ドル → 日本 輸入（20% 第1位，中国 x%）
米国 輸入（4.8%） ← 1482億ドル ← 日本 輸出（10% 第2位，中国 y%）
- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
米国の貿易赤字 685億ドル（≒9兆6000億円）
P. S. 7月10日付けでカナダ宛の手紙も公開された。税率上げる理由はフェンタニル。さらに，7月11日付けでメキシコとEUも。あとは中国（30%）①がどう決着するか。
23 カナダ 35%（25%）⑦
24 メキシコ 30%（25%）②
25 ＥＵ 30%（20%）⓪
登録:
投稿 (Atom)