感染症の数理シミュレーション(6)からの続き
動機
岩田健太郎さんが,
新型コロナウイルス感染症対策専門家会議(第5回)の参考資料「
新型コロナウイルス感染症の流行シナリオ(2 月 29 日時点)」を紹介していた。そこでは,基本再生産数$R_o=1.7$として,発病間隔を4日としていた。$\beta=1.7/4=0.42$であり,これらはこれまでの想定と矛盾しない。ところが入院期間や重症期間を15日と設定しており,これまでの$\gamma=5$という想定とは異なっている。そこで,前回の考察を見直したところ,導出根拠が不正確な部分があったので再検討する。
方針
中国の湖北省(武漢以外,人口4800万人)の感染データは感染者数が最も大きくほぼ収束しているデータである。新規確定感染者数 , 累計 $f(t) , g(t)=\int f(t) dt$と新規死亡数 , 累計 $h(t) , i(t)=\int h(t) dt$ が観測値として得られており,武漢のような特異性(突出した致死率)をもたない。そこで,これのデータを簡単な関数で近似して,SIIDR2モデルにあてはめることにより,モデルのパラメタである$\beta, \gamma_1, \gamma_2$を観測値から推定しようというものである。なお,前回の議論から$\alpha_1 = \dfrac{5}{0.8} = 6.25,\ \alpha_2 = \dfrac{5}{0.2} = 25,\ \dfrac{\alpha_2}{\alpha_1}=4$は前提とする。
SIIDR2モデル式($u_1 \approx n$, $\beta$=一定とした場合)
\begin{equation}
\begin{aligned}
u_1 &= n - \int \beta u_2 dt = n - 25 \beta g\\
u_2 &= 25 \beta g -5 g\\
u_3 &= \gamma_2 h\\
u_4 &= i\\
u_5 &= 4 g + \dfrac{\gamma_2}{\gamma_1} i \\
u_6 &= g
\end{aligned}
\end{equation}
これを$u_1+u_2+u_3+u_4+u_5=n$に代入して次式が得られる。
\begin{equation}
g(t) = \gamma_2 h(t) + (1+ \dfrac{\gamma_2}{\gamma_1}) i(t)
\end{equation}
この左辺と右辺がほぼ等しくなる$\gamma_1, \gamma_2$を探す。
観測値の近似式
湖北省(武漢以外)の観測値(1万人当りに換算)を再現するものとして前回と同様に次の近似関数を採用する。ただし,$h(t)$は前回から修正した。
\begin{equation}
\begin{aligned}
f(t) = t^4 \exp(-t/3) / 1600\\
g(t) = \int f(t) dt ; g(0)=0\\
h(t) = 1.4 t \exp(-(t - 20)^2/12^2) /4800\\
i(t) = \int h(t) dt ; i(0)=0
\end{aligned}
\end{equation}
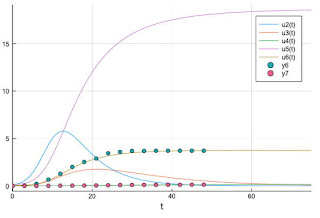
$h(t), i(t)$を24倍($\gamma_2/\gamma_1$)したグラフを$f(t), g(t)$と重ねたものを図1に示す。
図1 ピークと変曲点の時点が$t=12$の$f(t),\ g(t)$及び$t=24$の$h(t),\ i(t)$
最適値の検討
$r(t) = \{ \gamma_2 h(t) + (1+ \dfrac{\gamma_2}{\gamma_1}) i(t) \}/g(t)$を$t=10$から$t=30$の範囲でプロットして$r(t)$の値がほぼフラットであり平均して1前後になる$\gamma_1, \gamma_2$を探す。上記専門家会議の議論を踏まえて,$\frac{1}{\gamma}=\frac{1}{\gamma_1}+\frac{1}{\gamma_2}=\frac{1}{15}$とする。なお,これまでの$\gamma=5$を用いると$r(t)$が0.6あたりまで減ってしまう。結局,
\begin{equation}
\gamma_1 = \dfrac{15}{0.96}, \quad \gamma_2 = \dfrac{15}{0.04}
\end{equation}
このとき,$r(t)$の平均値として$\dfrac{1}{20} \int_{10}^{30} r(t) dt = 1.05$が得られるので,条件を満足している。
図2 $t=10$から$t=30$における$r(t)$の振る舞い
また前回の,$\beta(t)=\dfrac{df}{dt} / f + \dfrac{1}{\alpha}$についての議論はそのままであり変更されていないことに注意する。SIIDR2モデルを採用すれば,武漢(湖北以外)では$\beta(t)$を急速に小さくしたことが考えられる。なお,基本再生産率$R_o$と$\alpha$の値から$\beta$を一定とした場合の平均値は$\bar{\beta}=0.4 \sim 0.5$である。
湖北省(武漢以外)の1/20/2020から2/29/2020のデータを再現するSIIDR2モデルのパラメタとしては,次のセットが推奨される。
\begin{equation}
\alpha_1 = \dfrac{5}{0.8} ,\quad \alpha_2 = \dfrac{5}{0.2} ,\quad \bar{\beta}=0.4 \sim 0.5 ,\quad \gamma_1 = \dfrac{15}{0.96} ,\quad \gamma_2 = \dfrac{15}{0.04}
\end{equation}
付録 初期値$\nu$の取り扱い
これまでは,$u_2$の初期値を$\nu$としてきた。ところで,
各国の感染者比(1)と
各国の感染者比(2)から新規感染者数累計が人口の1ppmを越えた$t_0$を始点とするモデル化が必要があることがわかった。そこで,$t_0$における初期条件を再度検討する。はじめに$h(t_0)=i(t_0)=0$と近似した上で,上記関係式より,$u_2(t_0)=25 f(t_0), u_5(t_0)=4 g(t_0) , u_6(t_0)=g(t_0)$となる。ここで,$g(t_0)=\nu$と再定義する。$\nu$=1ppmが始点になる。
ところで,$f(t)=k t^m$と仮定すると
\begin{equation}
\begin{aligned}
g(t) &=\int f(t) dt = \dfrac{k t^{m+1}}{m+1}=\dfrac{t f(t)}{m+1}\\
\therefore f(t_0) &= \dfrac{m+1}{t_0} g(t_0) = \dfrac{m+1}{t_0} \nu
\end{aligned}
\end{equation}
したがって,$u_2(t_0)=\dfrac{25}{t_0}(m+1) \nu \approx 4\nu$となる。ただし,日本の1ppmに至るまでの観測値から,$t_0 \approx 25, m \approx 3$とおいた。
追加(3/17/2020)
次に,$u_3(t_0)$について考える。これは次の微分方程式を満たす。
\begin{equation}
\dfrac{du_3}{dt}=f -\dfrac{u_3}{\gamma}
\end{equation}
ここで,$u_3(t)=k t$と仮定して代入すると,$k = f -\dfrac{k t}{\gamma}$である。そこで,
$k=\dfrac{f(t_0)}{1+t_0/\gamma}$となる。上の結果から,$u_2(t_0)=25 f(t_0)$,したがって,次式が成り立つ。
\begin{equation}
u_3(t_0)= \dfrac{f(t_0)}{1+t_0/\gamma} t_0 = u_2(t_0) \dfrac{25}{t_0 (1+t_0/\gamma)}
\approx u_2(t_0) \dfrac{1}{(1+t_0/\gamma)} \sim \dfrac{1}{2} u_2(t_0) = 2\nu
\end{equation}
さらに
,$h(t_0)=i(t_0)=0$という条件をゆるめてみる。$u_3=\dfrac{u_2}{2}=375 h$より,$\int u_2 dt = 750 \int h dt = 750 i$,一方,$g = \int f dt = \dfrac{1}{25} \int u_2 dt$。したがって,$i = \dfrac{1}{30} g$となる。これから,$u_5(t_0)=4 g(t_0) + \dfrac{24}{30} g(t_0) \approx 5 \nu$となる。なお,$u_4(t_0)=i(t_0)= \dfrac{g(t_0)}{30} = \dfrac{\nu}{30} $なので,これはゼロのままとする。
この結果$u_1(t_0)=n-u_2(t_0)-u_3(t_0)-u_4(t_0)-u_5(t_0)=n-4\nu-2\nu-5\nu=n-11\nu$となり,新規感染者数累計が1ppmになる時点には,約11ppmの軽症感染者・重症感染者・死亡者・免疫獲得回復者が存在することになる。
- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
まとめると,$\nu$=1ppm時点の初期値を次のように設定する。
\begin{equation}
u_1(t_0)=n-11\nu, \quad u_2(t_0)=4\nu, \quad u_3(t_0)=2\nu, \quad u_4(t_0)=0, \quad u_5(t_0)=5\nu, \quad u_6(t_0)=\nu
\end{equation}
感染症の数理シミュレーション(8)に続く